Od autorów

Co znajdziemy w pakiecie PETSc?

• równań liniowych, metodami bezpośrednimi i iteracyjnymi;
• równań nieliniowych metodami typu Newtona;
• równań różniczkowych zwyczajnych metodami wielokrokowymi.

• procedury wysokiego poziomu, służące do manipulacji obiektami w rodzaju wektor, macierz, itp., niezależne od tego, czy pracujemy na komputerze sekwencyjnym, czy równoległym (to bardzo wygodne dla programisty!)
• dostęp do procedur niskiego poziomu do precyzyjnego zarządzania rozproszeniem danych pomiędzy procesorami, sposobu komunikacji, itd.

Przy tworzeniu kolejnych wersji biblioteki PETSc aktywnie uczestniczyli (i uczestniczą!) jej użytkownicy. Dlatego PETSc nie zapomina o wygodzie programisty i oferuje najrozmaitsze udogodnienia przydatne podczas uruchamiania aplikacji:

• zmianę parametrów i używanych metod bezpośrednio z linii komend;
• przyjazne przeglądarki do generowanych obiektów np. macierzy lub wektorów;
• system śledzenia (profiling) obliczeń zmiennoprzecinkowych i wykorzystania pamięci;
• rozległe możliwości wyłapywania błędów (debugging)
• środowisko graficzne.

Dlaczego warto poznać PETSc?

Optymalizacja pracy programistycznej

Pamiętajmy także, że ostateczną miarą rzeczywistej efektywności użytej metody rozwiązania danego problemu jest czas i koszt działania komputera plus czas i koszt pisania programu!

Eksperymenty numeryczne

Często, badając nowe algorytmy dla równań cząstkowych chcielibyśmy przeprowadzić eksperymenty, porównujące nasz algorytm z innymi dostępnymi. Łatwo to osiągnąć używając PETSc, ze względu na mnogość zaimplementowanych solverów i łatwość dodawania własnych, oraz możliwości profilingu: możemy zbadać nie tylko liczbę iteracji, ale także wymagania pamięciowe, koszt obliczeń, itp. Co więcej, prowadząc eksperymenty możemy szybko weryfikować w praktyce pewne hipotezy.

Równoległość

Jednym z istniejących rozwiązań jest język Fortran 90 oraz tworzony obecnie standard HPF. Fortran 90 w części zwalnia użytkownika od myślenia o równoległości, albowiem to kompilator może decydować, kiedy urównoleglić jakąś prostą operację. Tak na przykład działa kompilator F90 na Connection Machine CM-200. Podobne podejście stosuje np. Cray, gdzie jest dostępny tzw. zrównoleglacz kodu, dopisujący w programie odpowiednie dyrektywy dla kompilatora, powodujące wykorzystanie przetwarzania wektorowego lub równoległego.

Innym rozwiązaniem, jak sądzimy, bardziej elastycznym, jest wykorzystanie popularnego standardu MPI (Message Passing Interface) razem z "klasycznymi" językami programowania, takimi jak C czy Fortran. Właśnie ten drugi wariant wybrali autorzy PETSc, opierając na nim swoją implementację. PETSc daje z jednej strony dużo stosunkowo łatwych w użyciu narzędzi pozwalających na programowanie algorytmów równoległych bez potrzeby zagłębiania się w detale komunikacji między procesorami, itp. Z drugiej zaś strony, użytkownik wciąż może (jeśli chce) odzyskać pełną kontrolę nad realizacją przetwarzania równoległego i używać bezpośrednio funkcji standardu MPI.

Kiedy nie warto stosować PETSc?

Wydaje się nam także, iż raczej nie warto używać PETSc do zadań algebry liniowej z macierzami "gęstymi" (nawet dużego wymiaru). Lepiej skorzystać bezpośrednio z optymalizowanych bibliotek numerycznych, zazwyczaj dostarczanych przez producenta razem z superkomputerem, albo korzystać wprost z BLASów lub procedur LAPACKa czy ScaLAPACKa.

W końcu, wymieńmy parę wad PETSc. Zazwyczaj użycie PETSc prowadzi do wygenerowania kodu wynikowego o sporej objętości. Jest to problem, ale z drugiej strony, nawet najmniejszy program w PETSc daje nam wciąż dostęp do jej funkcjonalności i np. licznych procedur wychwytujących błędy. Również szybkość działania niektórych procedur zostawia trochę do życzenia. Poważną wadą PETSc jest dość stroma krzywa uczenia się: nie sposób zacząć programować w PETSc bez zapoznania się z manualem, a ten z kolei nie jest niestety najłatwiejszą lekturą...

Dlaczego i dla kogo napisaliśmy ten podręcznik?

Niniejszy podręcznik ma na celu po pierwsze - zainteresowanie tym nowoczesnym i wygodnym pakietem szerszego grona studentów, a także osób zajmujących się obliczeniami naukowymi/eksperymentami numerycznymi w Polsce, a po drugie - oszczędzenie początkującemu użytkownikowi PETSc mozolnego przegryzania się przez oficjalny manual i man pages: ułatwienie wstępnego zapoznania się z pakietem i szybkie (w miarę bezbolesne) umożliwienie mu rozpoczęcia pisania własnych programów wykorzystujących PETSc.

Adresujemy go przede wszystkim do tych osób, które chcą prowadzić eksperymenty numeryczne w dziedzinie równań różniczkowych cząstkowych typu eliptycznego, liniowych bądź nieliniowych. Dlatego ograniczyliśmy się wyłącznie do wersji sekwencyjnej PETSc, kwestiom równoległości poświęcając jedynie kilka komentarzy i uwag. Mimo to i tak objętość niniejszego podręcznika dorównuje blisko połowie objętości oficjalnego manuala, choć dotyczy jedynie 20% jego zawartości. Szczególny nacisk położyliśmy na zilustrowanie omawianych funkcji możliwie licznymi przykładami praktycznych zastosowań. Nie wszystkie przykłady są programami dającymi się uruchomić - często dla większej przejrzystości kodu zrezygnowaliśmy z linii nie związanych bezpośrednio z omawianym zagadnieniem. W każdym rozdziale znajdują się przykłady podsumowujące i te dadzą się skompilować i uruchomić. Ponieważ ten podręcznik ma jedynie pomóc w rozpoczęciu pracy z PETSc, nie będą też prezentowane i omawiane techniki związane z optymalizacją kodu pod kątem obliczeń równoległych. Jak wcześniej argumentowaliśmy, nawet w wersji sekwencyjnej (jednoprocesorowej) pakiet jest bardzo przydatnym narzędziem.

Jeśli będzie takie zapotrzebowanie, być może napiszemy kiedyś drugą część podręcznika, poświęconą technikom równoległym. Będziemy także wdzięczni za wszystkie uwagi dotyczące niniejszej wersji podręcznika. Prosimy je kierować pocztą elektroniczną na adres przykry@mimuw.edu.pl. Będziemy je uwzględniać w miarę możliwości w wersji elektronicznej podręcznika.

Aby korzystać z PETSc niezbędna jest znajomość w stopniu średnim programowania w języku C (podstawowe funkcje, wskaźniki, tablice i struktury) na poziomie standardu ANSI C. W zasadzie znajomość standardu Kernighan-Ritchie [12] też w zupełności wystarczy.

Podziękowanie

Wstęp

Aby rozwiązać powyższy układ przy pomocy komputera (być może równoległego) należy:

• Utworzyć wektory x i b i wpisać w wektor b odpowiednie wartości.
• Utworzyć i wpisać odpowiednie wartości w macierz A.
• Napisać procedury rozwiązywania takiego układu równań bądź metodą iteracyjną z preconditionerem, bądź bezpośrednią.
• Rozwiązać powyższy układ.

Inicjatorem projektu jest Barry Smith, który w 1991 roku napisał pierwszą wersję pakietu do rozwiązywania układów równań liniowych: PETSc 1.0. W ciągu kilku lat zestaw procedur przekształcił się w duży pakiet narzędzi do rozwiązywania równań różniczkowych cząstkowych, używany w wielu renomowanych ośrodkach obliczeniowych na świecie. Obecnie nad PETSc pracują Satish Balay, Willam Gropp, Lois Curfman McInnes i Barry Smith z Argonne National Laboratory (USA), wspomagani okazjonalnie przez grupy studentów - praktykantów. Akronim PETSc oznacza Portable, Extensible Toolkit for Scientific computation. Jak już wspomnieliśmy, pakiet jest w dużym stopniu niezależny od platformy sprzętowej. Programy można kompilować i uruchamiać na różnych architekturach, nie tracąc przy tym zbyt wiele z efektywności kodu, a jednocześnie wykorzystując potencjał konkretnego komputera. Obecnie obsługiwane architektury to:

• komputery osobiste klasy IBM PC, pracujące pod kontrolą systemów Linux, Windows 95 i NT 4.0;
• unixowe stacje robocze, z jednym lub kilkoma procesorami RISC: DEC Alpha, Silicon Graphics (także Origin i Power Challenge), Sun, IBM RS6000, itp.;
• sieć wyżej wymienionych komputerów połączonych Ethernetem;
• superkomputery masywnie równoległe (IBM SP2, Cray T3D/T3E, Convex Exemplar).

Drugim przymiotnikiem z nazwy jest Extensibile (rozszerzalny) - autorzy położyli duży nacisk na to aby pakiet był modularny i można było także wykorzystywać, ostatnio bardzo modne, programowanie obiektowe. "PETSc jest dowodem na to, że nowoczesne metody programowania mogą ułatwić rozwój wielkich aplikacji numerycznych w Fortranie, C i C++. Oprogramowanie, które tworzymy od kilku lat, rozwinęło się w potężny pakiet narzędzi do numerycznego rozwiązywania równań różniczkowych cząstkowych na superkomputerach" [2]. Warto dodać, że PETSc na pewno będzie dalej rozwijane przez parę najbliższych lat, jako że autorom pakietu przyznano grant rządowy. Każdy użytkownik pakietu może zwrócić się do autorów o pomoc, ponadto ma do dyspozycji listę dyskusyjną oraz sporo dodatkowych wydawnictw, głownie w formie elektronicznej. Szczegóły można znaleźć na stronie WWW poświęconej PETSc w Argonne National Laboratory: http://www.mcs.anl.gov/petsc/

Struktura PETSc

PETSc zawiera wiele składników podobnych do klas w C++. Każdy składnik dysponuje wydzieloną rodziną typów danych (na przykład wektorów) i operacji wykonywalnych na nich. Zarówno obiekty, jak operacje, opracowano na podstawie wieloletniego doświadczenia autorów (i użytkowników pakietu!) w rozwiązywaniu równań różniczkowych cząstkowych. Moduły PETSc operują obiektami takimi jak:

• wektory,
• macierze,
• iteracyjne i bezpośrednie solvery układów równań liniowych,
• preconditionery dla metod iteracyjnych,
• solvery zadań nieliniowych (na przykład metoda Newtona) oraz solvery zadań ewolucyjnych,
• urządzenia graficzne takie jak okna czy strony,
• zbiory indeksów, w tym permutacje,
• tablice rozproszone, użyteczne przy programowaniu równoległym.

W PETSc wszystkie funkcje nazywane są zgodnie z konwencją TypObiektuCzynność(), na przykład:

MatCreate() - generuje macierz

MatMult() - mnoży dwie macierze

VecAXBY() - wykonuje na wektorach operację 

OptionsGetInt() - pobiera z opcji zmienną typu int

Nazwy są długie, co nie oszczędza nam stukania w klawiaturę, ale za to większość nazw funkcji jest zrozumiała i łatwa do zapamiętania, co wspomaga pisanie i czytanie programów korzystających z biblioteki PETSc.

Jak czytać ten podręcznik?

Podręcznik składa się więc z dwóch części: w pierwszej wykładamy podstawy użytkowania PETSc i w oparciu o nie pokazujemy, jak można wykorzystać PETSc do rozwiązywania wielkich układów równań liniowych za pomocą nowoczesnych metod iteracyjnych. W drugiej części omawiamy bardziej zaawansowane techniki oraz metody wykorzystania PETSc do rozwiązywania układów równań nieliniowych. Obie części bogato ilustrujemy pouczającymi przykładami, związanymi najczęściej z eliptycznymi równaniami różniczkowymi cząstkowymi.

Wydaje się więc, że podręcznik ten trzeba czytać w sposób, hmm... monotoniczny, to znaczy "od początku do końca". Zachęcamy Czytelnika do pisania własnych programów i do testowania świeżo zdobytej wiedzy. W szczególności, dla dobrego wykonania ćwiczeń, którymi kończymy większość rozdziałów, warto jest zawsze zerknąć nie tylko do naszego podręcznika, ale też do man pages oraz oficjalnego manuala.

Nie da się ukryć, aby nauczyć się korzystać z PETSc, trzeba włożyć trochę wysiłku. Przede wszystkim, trzeba zacząć pisać programy. Dlatego zachęcamy do lektury poniższego pouczającego rozdziału.

Zaczynamy!

program1.c

#include "sles.h"
static char help[]="Najprostszy program uzywajacy PETSc\n";
int main(int argc,char **args)
{
 PetscInitialize(&argc,&args,PETSC_NULL,help);
 PetscPrintf(MPI_COMM_WORLD,"PETSc działa i pozdrawia\n"); 
 PetscFinalize();
}

hydra:/usr/home/students/bojko> program1
PETSc działa i pozdrawia
hydra:/usr/home/students/bojko> _

Mimo, że kod źródłowy jest bardzo krótki, skompilowanie tego programu spowoduje wygenerowanie dość dużego pliku wynikowego, a to dlatego, że do każdego programu dołączany jest szereg procedur ułatwiających życie programistom i użytkownikom - chociażby zestaw procedur do śledzenia pracy programu. Na przykład, uruchomienie tego samego programu z opcją -help spowoduje wypisanie:

hydra: /usr/home/students/bojko> program1 -help
--------------------------------------------------------------------------

PETSc Version 2.0.22, Released April 28, 1998.
The PETSc Team: Satish Balay, Bill Gropp, Lois Curfman McInnes, Barry Smith
 Bug reports, questions: petsc-maint@mcs.anl.gov
 Web page: http://www.mcs.anl.gov/petsc/
See docs/copyright.html for copyright information
See docs/changes.html for recent updates.
See docs/troubleshooting.html hints for problems.

See docs/manualpages/manualpages.html for help. 

Libraries linked from /usr/local/petsc/petsc-2.0.22/lib/libO/solaris

-----------------------------------------------------------------------

Options for all PETSc programs:
 -on_error_abort: cause an abort when an error is detected. Useful 
       only when run in the debugger
 -on_error_attach_debugger [dbx,xxgdb,ups,noxterm]
       start the debugger (gdb by default) in new xterm
       unless noxterm is given
 -start_in_debugger [dbx,xxgdb,ups,noxterm]
       start all processes in the debugger
 -debugger_nodes [n1,n2,..] Nodes to start in debugger
 -debugger_pause [m] : delay (in seconds) to attach debugger
 -display display: Location where graphics and debuggers are displayed
 -no_signal_handler: do not trap error signals

 -mpi_return_on_error: MPI returns error code, rather than abort on internal error
 -fp_trap: stop on floating point exceptions

           note on IBM RS6000 this slows run greatly
 -trdump: dump list of unfreed memory at conclusion
 -trmalloc: use our error checking malloc
 -trmalloc_off: don't use error checking malloc
 -trmalloc_nan: initialize memory locations with NaNs
 -trinfo: prints total memory usage
 -trdebug: enables extended checking for memory corruption
 -optionstable: dump list of options inputted
 -optionsleft: dump list of unused options
 -log[_all _summary]: logging objects and events
 -log_summary_exclude: <vec,mat,sles,snes>
 -log_trace [filename]: prints trace of all PETSc calls
 -log_info: print informative messages about the calculations
 -v: prints PETSc version number and release date
 -options_file <file>: reads options from file
-----------------------------------------------
Najprostszy program uzywajacy PETSc
PETSc działa i pozdrawia

hydra:/usr/home/students/bojko>_

Zanim rozpoczniemy nasze bliskie spotkanie z PETSc, jeszcze krótko omówimy sposób kompilowania i uruchamiania programów korzystających z biblioteki PETSc. Po pierwsze aby móc skompilować swój program należy ustawić zmienne środowiskowe PETSC_DIR, PETSC_ARCH, BLAS_DIR, LAPACK_DIR jak następuje:

setenv PETSC_DIR /usr/local/petsc/petsc-2.0.22
setenv PETSC_ARCH solaris
setenv BLAS_DIR /usr/local/petsc/blaslapack
setenv LAPACK_DIR /usr/local/petsc/blaslapack

makefile

BOPT=O
include $(PETSC_DIR)/bmake/$(PETSC_ARCH)/base
CFLAG          = $(CPPFLAGS) -D__SDIR__='"$(LOCDIR)"' $(BS_INCLUDE)
LIBBASE        = libpetscsles
LOCDIR         = /usr/home/students/bojko/source/

program1:  program1.o  
           -$(CLINKER) -o program1 program1.o  $(PETSC_LIB)
            $(RM) program1.o

Ćwiczenia

1. W katalogu $PETSC_DIR/docs znajdują się: manual [2] oraz man pages [3] dla PETSc, w formacie HTML. Odnajdź te pliki i przejrzyj ich zawartość przy użyciu jakiejś przeglądarki do stron WWW (np. Netscape). Będziesz ich bardzo często potrzebować, więc warto.
2. Ten podręcznik też ma swoje wcielenie internetowe. Łatwo stamtąd ściągniesz omawiane tu kody źródłowe i Makefile. Ponadto, właśnie tam będziemy umieszczać wszelkie poprawki i uaktualnienia. Zobacz http://www.mimuw.edu.pl/~przykry/petsc/podrecznik.html
3. Skompiluj i uruchom przykładowy program używający biblioteki PETSc. W przypadku kłopotów skontaktuj się z jakimś bardziej doświadczonym użytkownikiem pakietu. Warto poświęcić chwilę czasu na ustawienie (raz, a dobrze!) zmiennych środowiskowych i napisanie własnego Makefile. Zaprocentuje to w przyszłości!
4. Na przykładzie programu "PETSc działa i pozdrawia" zobacz, jak działają inne opcje PETSc, w szczególności: -log, -v, -trinfo.

I. Rozwiązywanie układów równań liniowych

W tej części zostanie omówiony sposób rozwiązywania układów algebraicznych równań liniowych przy użyciu pakietu PETSc. Na początku opisane zostaną podstawowe struktury w PETSc: skalary, wektory i macierze, potrzebne do zbudowania zagadnienia. Potem wprowadzony zostanie SLES - obiekt PETSc, pozwalający na rozwiązanie układu równań liniowych . Pozwoli to na uruchomienie prostego programu rozwiązującego układ równań powstałych z dyskretyzacji zagadnienia Poissona

metodą różnic skończonych.

Następnie omówione zostaną szczegółowo struktury PETSc pozwalające na wybór metod iteracyjnych i włączanie w nie preconditionerów (także własnych). Ostatni rozdział poświęcony zostanie na szczegółowy opis istniejącego w pakiecie preconditionera addytywnej metody Schwarza, wykorzystującego metodę dekompozycji obszaru.

Skalary

Wektory

Podstawy

...
Vec X;
...

Najprostszą funkcją służącą do wygenerowania wektora jest funkcja:

Pierwszy argument to informacja dla MPI (Message Passing Interface) o sposobie komunikacji między procesami. Nie warto zagłębiać się w subtelności z tym związane. Ważne jest, że z argumentem MPI_COMM_WORLD funkcja działa poprawnie zarówno na maszynach wieloprocesorowych, jak i jednoprocesorowych i we wszystkich podobnych przypadkach rozważanych w tym podręczniku będzie używana ta właśnie wartość. Drugi argument, n, jest liczbą elementów wektora przechowywanych w procesorze, który wywołał funkcję; możemy podać wartość PETSC_DECIDE, gdy chcemy aby pakiet ustawił tę wielkość automatycznie. PETSC_DECIDE jest idealną wartością dla n, gdy program nasz ma działać przede wszystkim w wersji sekwencyjnej. Trzeci argument, N, jest liczbą współrzędnych całego wektora (można wstawić PETSC_DETERMINE, wtedy zostanie ona określona na podstawie liczby procesorów i wartości n). Ostatnim argumentem jest wskaźnik do zmiennej typu wektor. Wektor będzie składał się ze współrzędnych typu Scalar.

...
VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,100,&X);
...

...
double x[100]; 
...

...
double *x;
...
x=(double*)calloc(100,sizeof(double));
...

Funkcja VecCreate() jest zaprojektowana tak, aby automatycznie rozproszyć wektor pomiędzy dostępne procesory (procesy). Pakiet sam zadecyduje czy wygenerować wektor sekwencyjny, czy równoległy, a jeśli równoległy, to ile elementów wektora będzie przechowywanych w poszczególnych procesorach.

Po wygenerowaniu wektora można przypisać wartości poszczególnym współrzędnym. Służą do tego dwie funkcje: VecSet(Scalar *val, Vec X) która nada wszystkim współrzędnym jednakową wartość val lub funkcja VecSetValue(Vec X, int idx, Scalar val, InsertMode mode). Pierwszy argument tej funkcji to wektor w który wstawiamy wartość, drugi to numer współrzędnej, trzeci wartość na tej współrzędnej. Czwarty argument to tryb wstawiania wartości, Możliwe są dwie wartości: ADD_VALUES - dodaj wartość do istniejącej, INSERT_VALUES - wstaw nową wartość.

Przykład

a na końcu wektor zostanie wypisany na konsolę.

#include "sles.h"
static char help[]="przyklad2\n";

int main(int argc,char **args)
{
  Vec     x; 
  Scalar val;
  int i,n=10;

  /* inicjalizacja */
  PetscInitialize(&argc,&args,PETSC_NULL,help);

  /* wygenerowanie wektora */
  VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,n,&x);
  
  /* przypisanie wartosci */
  for(i=0;i<n;i++)
  {
   if(i>0)val=(Scalar)1/i; else val=1;
   VecSetValue(x,i,val,INSERT_VALUES);
  }

  /* wypisuje wektor na konsolę */
  VecView(x,VIEWER_STDOUT_SELF);


  /* zakończenie */
  VecDestroy(x);
  PetscFinalize();
  return(0);
 }

hydra:/usr/home/bin/> przykład
1
1
0.5
0.333333
0.25
0.2
0.166667
0.142857
0.125
0.111111
hydra:/usr/home/bin/> _

Po zadeklarowaniu, wygenerowaniu i przypisaniu wartości wektorowi x, na zakończenie programu wypisujemy go na ekran przy użyciu przeglądarki do wektorów VecView().

Co jeszcze warto wiedzieć

Aby wygenerować kilka takich samych wektorów (na przykład wektor rozwiązania równania i wektor prawej strony - oba są tego samego rozmiaru) można użyć funkcji VecDuplicate(Vec stary,Vec *nowy) lub VecDuplicateVecs(Vec stary,int n, Vec **nowe) pierwsza z tych funkcji utworzy wektor nowy o takiej samej strukturze jak wektor stary, to znaczy o tym samym rozmiarze i tak samo rozproszony pomiędzy procesorami. Druga utworzy n nowych wektorów o takiej samej strukturze jak stary i zapisuje w tablicy wektorów nowe. Powielenia struktury wektora nie należy mylić z kopiowaniem jego wartości. Do tego służy funkcja VecCopy(Vec x,Vec y), kopiująca wartości z wektora x do y. Wektory x i y musza w tym wypadku mieć taką samą strukturę, co znaczy, że uprzednio muszą być utworzone, na przykład przy pomocy funkcji VecCreate() lub VecDuplicate().

Nie istnieje, niestety, funkcja VecGetValues(), która pozwalałaby na pobranie wartości z wektora. W przypadku równoległym trzeba stosować specjalne funkcje zbierające i rozsyłające dane po procesorach. W przypadku sekwencyjnym można używać funkcji VecGetArray(Vec x,Scalar **val), która zwraca wskaźnik do tablicy elementów wektora przechowywanych w procesorze który wywołał tę procedurę. Po zakończeniu wszelkich operacji na tablicy elementów trzeba ją z powrotem wstawić do wektora funkcją VecRestoreArray(Vec x, Scalar **val).

Przydatna jest też funkcja VecView(Vec v, Viewer viewer), która pokazuje wektor v przy pomocy przeglądarki viewer. Istnieją trzy predefiniowane przeglądarki:

Gdy wektor nie jest już potrzebny, należy zwolnić pamięć którą zajmuje funkcją VecDestroy(Vec x) lub - w przypadku tablicy wektorów - VecDestroyVecs(Vec *wektory,int n). 

Podstawowe operacje wektorowe

Nazwa funkcji	Operacja
VecAXPY(Scalar *a,Vec x,Vec y);
VecAYPX(Scalar *a,Vec x,Vec y);
VecWAXPY(Scalar *a,Vec x,Vec y,Vec w);
VecScale(Scalar *a,Vec x);
VecDot(Vec x,Vec y,Scalar *r);
VecTDot(Vec x,Vec y,Scalar *r);
VecNorm(Vec x,NormType norm,Double *r);  norm{NORM_1,NORM_2,NORM_INFINITY}
VecSum(Vec x, Scalar *r);
VecCopy(Vec x, Vec y);
VecSwap(Vec x, Vec y);
VecPointwiseMult(Vec x, Vec y, Vec w);
VecPointwiseDivide(Vec x, Vec y, Vec w);
VecMax(Vec x, int *idx, double *r);
VecMin(Vec x, int *idx, double *r);
VecAbs(Vec x);
VecReciprocal(Vec x);
VecShift(Scalar *s, Vec x);

Podsumowanie

• Zadeklarować zmienną typu Vec
• Utworzyć wektor funkcją VecCreate()
• Wstawić wartości funkcją VecSetValues(), po czym wywołać funkcje VecAssemblyBegin() i VecAssemblyEnd()
• Po użyciu wektora, zwolnić zajmowaną przezeń pamięć funkcją VecDestroy()

Przykład podsumowujący

static char help[]="przyklad 4.6";
#include "sles.h"
#include <stdio.h>

int main(int argc,char **args)
{
  Vec     x,y; 
  Scalar  val,*wartosci;
  int     i,n=5,*indeksy,flg;

  PetscInitialize(&argc,&args,PETSC_NULL,help);
  
  VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,n,&x);
  VecDuplicate(x,&y);
  indeksy=(int*)calloc(n/2,sizeof(int));
  wartosci=(Scalar*)calloc(n/2,sizeof(Scalar));
  val=0.5;
  VecSet(&val,x);
  VecView(x,VIEWER_STDOUT_SELF);
  PetscPrintf(MPI_COMM_WORLD,"\n");
  VecCopy(x,y);

/* przygotowanie danych */
  for(i=0;i<n/2;i++)
  {
   if(i>0)wartosci[i]=(Scalar)1/i; 
   else wartosci[i]=1;
   indeksy[i]=2*i;
  }

/* Wstawienie danych do wektora */
  VecSetValues(y,n/2,indeksy,wartosci,ADD_VALUES);
  VecAssemblyBegin(y);
  VecAssemblyEnd(y);
  VecView(y,VIEWER_STDOUT_SELF);
  PetscPrintf(MPI_COMM_WORLD,"\n");  

/* policzenie różnicy dwóch wektorów */
  val=-1;
  VecAXPY(&val,x,y);

/*wypisanie wektorów */
  VecView(y, VIEWER_STDOUT_SELF);
  PetscPrintf(MPI_COMM_WORLD,"\n");

/*zakończenie*/
  VecDestroy(x);
  VecDestroy(y);
  free(indeksy);
  free(wartosci);
  PetscFinalize();
  return(0);
 }

hydra:/usr/home/> przyklad
0.5
0.5
0.5
0.5
0.5

1.5
0.5
1.5
0.5
0.5

1
0
1
0
0

hydra:/usr/home/> _

Ćwiczenia

1. Utwórz na dwa sposoby (VecSetValue()+ pętla lub VecSet()) wektor o 10 współrzędnych wszystkich równych a) 1, b), Obejrzyj te wektory na konsoli i w okienku graficznym. (Uwaga: w pliku <math.h> jest zdefiniowana stała M_PI zawierająca przybliżenie )
2. Utwórz wektor x o N współrzędnych równych . (Zauważ, że taki wektor można potraktować jako dyskretyzację funkcji na odcinku [0,1]). Obejrzyj ten wektor na konsoli i w okienku graficznym. Eksperymentuj dla różnych wartości N.
3. Utwórz wektor y o NxN współrzędnych . Przez analogię z poprzednim można ten wektor traktować jako dyskretyzację funkcji na kwadracie [0,1]² z siatką o kroku h = 1/(N-1). Obejrzyj y w okienku graficznym. Zobacz jak trudno zgadnąć, jaką funkcję dyskretyzuje y, stąd wniosek, że do takiej wizualizacji trzeba używać innych narzędzi. Dowiedz się, jakie programy wizualizacyjne są dostępne na Twoim komputerze i jak z nich korzystać.
4. Oblicz normy a), b), c)wektorów x i y z poprzednich ćwiczeń. Jakich relacji między tymi normami można się spodziewać?
5. Zwróć uwagę, że dyskretna norma l₂ funkcji siatkowej reprezentowanej przez wektor x to odpowiednio przeskalowana norma euklidesowa tego wektora. Napisz procedurę, obliczającą normę l₂ wektora siatkowego x określonego na siatce o kroku h i N węzłach. Sprawdź na poprzednich przykładach, jak zachowuje się ta norma, gdy N rośnie. Porównaj to z normami: euklidesową i "max".
6. Wygeneruj wektor o długości 5 i losowych współrzędnych z przedziału [-1,1]. Będzie do tego potrzebna funkcja PetscRandom() której opis znajduje się w man pages [3].
7. Napisz funkcję VecGetValues(Vec v,int n,int *ind, Scalar *val), która z wektora wyciąga n kolejnych wartości.

Macierze

Po zadeklarowaniu zmiennej jako macierz:

...
Mat A;
...

należy utworzyć, podobnie jak w przypadku wektorów, obiekt typu macierz. Robi się to przy pomocy funkcji: MatCreate(MPI_Comm comm,int m,int n,Mat *A).Funkcja tworzy macierz A o rozmiarze , gdzie m to liczba wierszy, a n kolumn. Wstawianie wartości do macierzy odbywa się analogicznie jak w przypadku wektorów, przy pomocy funkcji MatSetValue(Mat A,int row,int col,Scalar val,InsertMode mode). Ta funkcja wpisuje w macierz A wartość val w miejsce row,col. Ostatni argument określa, podobnie jak w przypadku wektorów, sposób wstawiania wartości do macierzy i może przyjąć wartości INSERT_VALUES lub ADD_VALUES. Do zwolnienia pamięci zajmowanej przez macierz służy funkcja MatDestroy(Mat A), która działa tak samo jak jej odpowiednik dla wektorów.

Przykład

#include "sles.h"

static char help[]="przykład_3\n";
int main(int argc,char **args)
{
  Mat     A; 
  int i,n=5;
  /* inicjalizacja */
  PetscInitialize(&argc,&args,PETSC_NULL,help);
  /* wygenerowanie macierzy trójdiagonalnej*/
  MatCreate(MPI_COMM_WORLD,n,n,&A);

  /* wypełniamy macierz wierszami */
  for(i=0;i<n;i++)
  {
   MatSetValue(A,i,i,2,INSERT_VALUES);
   if(i<n-1)MatSetValue(A,i,i+1,1,INSERT_VALUES);
   if(i>0)MatSetValue(A,i,i-1,1,INSERT_VALUES);
  }
  MatAssemblyBegin(A,MAT_FINAL_ASSEMBLY);
  MatAssemblyEnd(A,MAT_FINAL_ASSEMBLY);
  
  /* wypisuje macierz na konsolę */
  MatView(A,VIEWER_STDOUT_SELF);
  
  /* zakończenie */
  MatDestroy(A);
  PetscFinalize();
  return(0);
 }

hydra:/usr/home/bin/> przykład
row 0: 0 2  1 -1 
row 1: 0 -1  1 2  2 -1 
row 2: 1 -1  2 2  3 -1 
row 3: 2 -1  3 2  4 -1 
row 4: 3 1  4 2 

hydra:/usr/home/bin/> _

Rysunek 1. Działanie funkcji MatSetValues().

Przyjrzyjmy się, jak działa przeglądarka macierzy MatView() w trybie tekstowym: macierz jest wypisywana wierszami. W każdym wierszu podawane są tylko niezerowe elementy (bardzo słusznie!); dlatego format wydruku jest następujący:

...
row wiersz: kolumna wartość kolumna wartość kolumna wartość
....

Co jeszcze warto wiedzieć

Ta funkcja rozprasza w macierzy A macierz o rozmiarze mxn zapisaną w tablicy val w miejsca zapisane w tablicach row i col. Sposób działania tej funkcji wyjaśnia rysunek 1.

Aby wartości zostały fizycznie wpisane do macierzy należy, zawsze wywołać funkcje: MatAssemblyBegin(Mat A,MatAssemblyType type) i MatAssemblyEnd(Mat A, MatAssemblyType type). Zmienna type może przyjąć dwie wartości: MAT_FLUSH_ASSEMBLY bądź MAT_FINAL_ASSEMBLY. Pierwsza wartość jest używana, gdy zmieniamy tryb wstawiania wartości (INSERT_VALUES na ADD_VALUES, bądź na odwrót), druga - gdy kończymy wstawianie wartości i macierz ma zostać użyta.

Rysunek 2. Macierz trójdiagonalna z poprzedniego przykładu w przeglądarce graficznej.

Funkcja MatCreate() tworzy szkielet macierzy rozrzedzonej pewnego (domyślnego) rodzaju. Użytkownik może też samemu wpłynąć na sposób generowania macierzy. Na przykład, można zaznaczyć jak duże kawałki macierzy mają być przechowywane w poszczególnych procesach, czy też, jak macierze mają być składowane: wierszami czy kolumnami. Szczegółowy opis można znaleźć w manualu [2] i man pages [3]. Dla potrzeb początkującego użytkownika przydatna jest jeszcze funkcja MatCompress(Mat A), która poddaje macierz kompresji, tak aby zajmowała jak najmniej miejsca w pamięci, gdyż funkcja MatCreate alokuje 10 razy ilość wierszy macierzy, co z reguły jest za dużo. Warto zatem po zakończeniu wpisywania wartości i wywołaniu funkcji MatAssemblyEnd(), wywołać funkcję MatCompress(). W przypadku gdy wiemy, że macierz zajmie więcej miejsca niż domyślne "10 razy ilość wierszy" trzeba użyć funkcji MatCreateSeqAIJ(), lub podobnej, ponieważ alokowanie dodatkowego miejsca w czasie wstawiania wartości do macierzy może spowodować nawet 50 krotne (!) spowolnienie działania funkcji.

Jak już wspomnieliśmy, dla macierzy istnieje funkcja MatView(Mat A,Viewer view), która pokazuje macierz w przeglądarce. Przeglądarka VIEWER_DRAWX_WORLD pokazuje, w okienku graficznym, strukturę niezerowych miejsc macierzy. Rysunek 2 pokazuje efekt przeglądania w trybie graficznym macierzy z poprzedniego przykładu.

Podstawowe operacje macierzowe

Nazwa funkcji	Operacja
MatEqual(Mat A,Mat B)	sprawdza czy A=B
MatMult(Mat A, Vec x, Vec y)
MatMultAdd(Mat A, Vec x,Vec y, Vec z)
MatMultTrans(Mat A, Vec x,Vec y)
MatMultTransAdd(Mat A, Vec x,Vec y, Vec z)

Podsumowanie

• Zadeklarować zmienną typu Mat
• Utworzyć strukturę macierzy funkcją MatCreate() (lub inną funkcją, pozwalającą na podanie przypuszczalnego współczynnika zapełnienia macierzy).
• Wstawić do macierzy wartości funkcją MatSetValues()
• Wywołać funkcje MatAssemblyBegin() i MatAssemblyEnd() (z opcją FINAL_ASSEMBLY)
• Gdy macierz nie jest już potrzebna, zwolnić pamięć funkcją MatDestroy()

Przykład podsumowujący

po czym mnożony jest przez nią wektor złożony z samych jedynek, a efekt zostaje wypisany na konsolę.

#include "sles.h"

int main(int argc,char **args)
{
  Vec     x,y;
  Mat     A; 
  int     i,k,l,n=4,m=4,flg,col[5];
  Scalar  val[5];

/* inicjalizacja */
  PetscInitialize(&argc,&args,PETSC_NULL,PETSC_NULL);

/* wektory przydatne przy demonstracji */
  VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,n*m,&x);
  VecDuplicate(x,&y);
  val[0]=1.0;
  VecSet(val,x);

/* Tworzenie macierzy laplasjanu na prostokacie mxn */
  MatCreate(MPI_COMM_WORLD,n*m,n*m,&A);
  val[0] = -1.0; val[1] = -1.0; val[2] = 4.0;
  val[3]=-1.0;val[4]=-1.0;
  for (i=0; i<n*m; i++ ) 
  {
    col[0]=i+1; col[1]=i-1; col[2]=i;
    col[3]=i+m; col[4]=i-m;
    l=0;k=5;
    if(i<m)k=4;
    if((i+1)>(n-1)*m){k=4;col[3]=i-m;}
    if((i%m)==0){l=1;k=k-1;col[1]=i+1;}
    if((i+1)%m==0)if(i!=0){l=1;k=k-1;}
    MatSetValues(A,1,&i,k,&col[l],&val[l],INSERT_VALUES);
  }

/* Składanie macierzy*/
  MatAssemblyBegin(A,MAT_FINAL_ASSEMBLY);
  MatAssemblyEnd(A,MAT_FINAL_ASSEMBLY);

/*Mnożenie wektora x przez macierz A (y=A*x)*/
  MatMult(A,x,y);

/*Wypisanie wektora y na konsolę*/
  VecView(y,VIEWER_STDOUT_SELF);

/* zakończenie */
  VecDestroy(x);
  MatDestroy(A);
  PetscFinalize();
  return(0);
 }

hydra:/usr/home/>p5.6
2
1
1
2
1
0
0
1
1
0
0
1
2
1
1
2
hydra:/usr/home/> _

Macierze powłokowe

jest macierzową reprezentacją (w standardowej bazie R³) następującego operatora:

Taka definicja jest szczególnie ważna w przypadku macierzy rozrzedzonych, w których powtarzają się elementy, gdyż dzięki temu nie musimy tracić miejsca w pamięci na powtarzające się wartości. Na przykład macierz powstała z dyskretyzacji jednowymiarowego laplasjanu ma (z dokładnością do stałej) postać:

Działanie tą macierzą na wektor można zapisać następująco:

,

gdzie

Autorzy pakietu przewidzieli możliwość definiowania macierzy w ten sposób. Użytkownik informuje pakiet jedynie o rozmiarze macierzy i podaje poszczególne funkcje realizujące operacje na tej macierzy (czy tą macierzą). Istotne jest to, że taka macierz jest traktowana tak samo jak inne rodzaje macierzy. Dopóki program nie usiłuje wykonać na nich operacji niewykonalnej, to znaczy nie zdefiniowanej przez użytkownika, to nie ma absolutnie żadnej różnicy w posługiwaniu się tą macierzą i macierzą "zwykłą". Macierze definiowane w duchu operatorowym zwane są powłokowymi (ang. shell matrix).

Mając zadeklarowaną zmienną typu Mat, możemy utworzyć ją w postaci macierzy powłokowej. Do tego służy funkcja:
MatShellCreate(MPI_Comm com,int m,int n,int M,int N,void *ctx,Mat *mat)

Pierwszy argument to kanał komunikacyjny MPI (np. MPI_COMM_WORLD), drugi i trzeci argument (m i n) to rozmiar lokalny macierzy, to znaczy rozmiar części macierzy zapisanej w procesorze wywołującym tę funkcję. Czwarty i piąty argument (M i N) to globalny rozmiar macierzy. Oczywiście, w wersji sekwencyjnej będziemy mieli n=N i m=M; ponadto (zazwyczaj) nasze macierze będą kwadratowe więc wtedy dodatkowo m=n=M=N. Szósty argument (ctx) to wskaźnik do kontekstu związanego z macierzą, lub PETSC_NULL, gdy nie korzystamy z kontekstu. Ostatni argument to wskaźnik do zmiennej typu Mat z którą będzie powiązana macierz powłokowa.

Do definiowania operacji, którą można wykonać na macierzy powłokowej służy funkcja:

MatShellSetOperation(Mat mat,MatOperation op, void *f)

Pierwszy argument tej funkcji to zmienna powiązana z obiektem typu Mat, dla którego definiujemy operację. Drugi argument to nazwa operacji, a trzeci to wskaźnik do funkcji wykonującej tą operację. Zdefiniować można 63 operacje, w poniższej tabeli podanych jest kilka ważniejszych:

MATOP_MULT

MATOP_EQUAL

MATOP_GET_SIZE

MATOP_DESTROY

MATOP_VIEW

MATOP_NORM

MATOP_GET_DIAGONAL

MATOP_DIAGONAL_SCALE

MATOP_SET_VALUES

Przykłady

Przykład trywialny

#include "sles.h"
#define N=100

/****************************************************
                Procedura mnozenia przez macierz
****************************************************/

int mult(Mat A,Vec x,Vec y)
{
 VecCopy(x,y);
 return(0);
}

/****************************************************
                Program glowny
****************************************************/
main(int argc,char **args)
{
 Mat A;
 Vec v,b;
 PetscInitialize(&argc,&args,PETSC_NULL,PETSC_NULL);

 /* ...pominiete linie kodu: tworzenie wektora b i przypisanie mu
    wartosci... */

 /* tworzenie macierzy powłokowej */
 MatCreateShell(MPI_COMM_WORLD,N,N,N,N,PETSC_NULL,&A);
 MatShellSetOperation(A,MATOP_MULT,mult);

 /* zastosowanie */
 MatMult(A,v,b); 
 PetscFinalize();
}

Dyskretny laplasjan

#include "sles.h"
#include <stdio.h>

/****************************************************
      Procedura mnozenia przez macierz
****************************************************/
int mult(Mat A,Vec x,Vec y)
{
 int i,N,*idx;
 Scalar *wx,*wy;

 VecGetSize(x,&N);
 VecGetArray(x,&wx);
 VecGetArray(y,&wy);
 for(i=0;i<N;i++)
 { 
  wy[i] = 2*wx[i];
  if(i>0) wy[i] -= wx[i-1];
  if(i<N) wy[i] -= wx[i+1];
 }
 VecRestoreArray(x,&wx);
 VecRestoreArray(y,&wy); 
}
/****************************************************
                    Program glowny
****************************************************/
int main(int argc,char **args)
{
 Mat A;
 int N=10;
 Scalar val;
 Vec x,y;

 PetscInitialize(&argc,&args,PETSC_NULL,PETSC_NULL);

 /* tworzenie macierzy powłokowej */
 MatCreateShell(MPI_COMM_WORLD,N,N,N,N,0,&A);
 MatShellSetOperation(A,MATOP_MULT,mult);

 /* Wektory przydatne przy prezentacji */
 VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,N,&x);
 VecDuplicate(x,&y);
 val=1; 
 VecSet(&val,x);
 
 /* uzycie macierzy powlokowej */
 MatMult(A,x,y);
 VecView(y,VIEWER_STDOUT_SELF);

 /* Zakończenie */
 VecDestroy(x); VecDestroy(y);
 MatDestroy(A);
 PetscFinalize();
 return(0);
}

hydra:/usr/home/> przykład
1
0
0
0
0
0
0
0
0
1
hydra:/usr/home/> _

Ćwiczenia

1. Uruchom program z przykładu trywialnego dla różnych N i dodaj przeglądarki wektorów, dzięki której będzie można obejrzeć wektor przed i po mnożeniu przez macierz. Proponujemy także zaimplementowanie innej macierzy diagonalnej w postaci macierzy powłokowej, np.:

2. Wygeneruj macierz NxN:


obejrzyj ją w okienku, a następnie na konsoli. Naucz się odczytywać te widoki.

3. Przeskaluj macierz A o czynnik , gdzie . Napisz procedurę GenLap1D(Mat A, int h) która generuje macierz NxN dyskretyzacji 1-wymiarowego Laplasjanu.
4. Zrób to samo co w poprzednim ćwiczeniu, ale macierz zaimplementuj jako macierz powłokową.
5. Wygeneruj macierz dyskretyzacji operatora


metodą różnic skończonych. Wskazówka: użyj funkcji GenLap1D() a następnie dodaj wartości pochodzące z dyskretyzacji pierwszej pochodnej.

6. Obejrzyj macierz z poprzedniego ćwiczenia, następnie transponuj ją i znów obejrzyj.
7. Napisz funkcję tworzącą macierz dyskretyzacji pierwszej pochodnej różnicą centralną


Użyj obu macierzy do dyskretyzacji operatora L z ćwiczenia E) w wersji



(Najwygodniej zdefiniować go jako macierz powłokową!)

8. Napisz procedurę rozwiązywania układu z daną macierzą, metodą Richardsona z preconditionerem Jacobiego. Użyj funkcji MatGetDiag() do wyciągnięcia diagonali, a całą procedurę zaimplementuj używając funkcji wektorowych VecAXPY(), VecScale(), VecPointwiseDivide().
9. Zaprogramuj własną przeglądarkę do macierzy/wektorów, używając procedur graficznych PETSc, tak, aby każde wywołanie otwierało nowe okno, utrzymujące się do końca pracy programu.
10. Procedura z ćwiczenia G wymaga pewnych obiektów pomocniczych wektorów roboczych do przechowywania wyników pośrednich. Zastanów się jak to zgrabnie zaimplementować. Zajrzyj do rozdziału "Koncept kontekstu" na stronie 58.
11. Trudne zadanie, ale warto. Zaimplementuj procedurę generującą macierz sztywności dla dyskretyzacji równania eliptycznego drugiego rzędu na zadanej triangulacji MES i rozmaitych elementów skończonych. Oczywiście, zgodnie z prawidłami sztuki, najpierw skonstruuj lokalne macierze sztywności, które potem złożysz w globalną macierz sztywności w procesie assemblacji. Znakomicie pasuje tu funkcja MatSetValues().

SLES, czyli rozwiązywanie układów równań liniowych

Aby go rozwiązać, musimy utworzyć wektory rozwiązania i prawej strony oraz macierz zadania, a następnie spiąć te wszystkie dane ze sobą i zlecić pakietowi rozwiązanie tego układu. Do tego służą właśnie obiekty typu SLES.

Aby utworzyć obiekt typu SLES trzeba, podobnie jak w poprzednich przypadkach, najpierw zadeklarować odpowiednią zmienną:

...
SLES MojSles;
...

Pierwszy argument funkcji SLESCreate() to, podobnie jak w przypadku innych obiektów, kanał komunikatora MPI, u nas zawsze będzie to MPI_COMM_WORLD. Drugi to wskaźnik do uprzednio zadeklarowanej zmiennej typu SLES.

Następną czynnością, jaką należy wykonać, jest przekazanie macierzy zadania do SLESu. Robi się to przy pomocy funkcji:

SLESSetOperators(SLES MojSles,Mat A,Mat P, MatStructure flag);

Powyższe przygotowania wystarczają, aby SLES rozwiązał układ równań z macierzą A i prawą stroną b. W tym celu należy wywołać funkcję SLESSolve(SLES MojSles,Vec b,Vec x,int *its). Wynik zostanie zapisany w wektorze x.

W zmiennej its zostanie zapisana liczba wykonanych iteracji. Po zakończeniu obliczeń należy zwolnić pamięć zajmowaną przez SLES funkcją: SLESDestroy(SLES MojSles), gdzie argumentem jest (niepotrzebny już) obiekt MojSles. Ważne jest, że jeden SLES może służyć do rozwiązania wielu układów równań, na przykład kilku układów z tą samą macierzą i inną prawą stroną.

Podsumowanie

• Zadeklarować zmienne Mat A; Vec b,x; i SLES MojSles;
• Utworzyć wektor rozwiązania x i wektor prawej b strony, a następnie wpisać w b odpowiednie wartości (szczegóły w rozdziale 2 na stronie 9)
• Utworzyć macierz zadania A i wpisać w nią odpowiednie wartości.
• Utworzyć obiekt typu SLES funkcją SLESCreate()
• Przekazać macierz zadania i preconditionera do SLESu funkcją SLESSetOperators()
• Rozwiązać zadanie funkcją SLESSolve()
• Po rozwiązaniu, gdy już obiekt jest niepotrzebny, należy zwolnić pamięć funkcją SLESDestroy()

Przykład

#include "sles.h"

int main(int argc,char **args)
{
  Vec    x,b;
  Mat    A;            /* macierz układu równań */
  SLES   MojSles;         /* kontekst SLESu */
  int    its;
  Scalar val;

  PetscInitialize(&argc,&args,PETSC_NULL,PETSC_NULL);

/* Tworzenie kontekstu SLES */
  SLESCreate(MPI_COMM_WORLD,&MojSles); 

/* tutaj trzeba utworzyć wektory (str. 12)
   i macierze, (str. 17) */

/*Ustawienie operatorów */
  SLESSetOperators(MojSles,A,A,DIFFERENT_NONZERO_PATTERN); 
  SLESSetFromOptions(MojSles);

/* rozwiązanie układu liniowego */
  SLESSolve(MojSles,b,x,&its);

/*Tu z kolei należy zwolnić pamięć*/
  SLESDestroy(MojSles);
  PetscFinalize();
  return(0);
}

Ćwiczenia

1. Rozwiąż równanie


na siatce o kroku h. Testuj błąd rozwiązania w normie max i l₂ dla f odpowiadającym rozwiązaniu dokładnemu
a) sin(x),
b) x²+y².
Sprawdź, jak zmienia się liczba iteracji w zależnościod h. Obejrzyj wektory rozwiązania i błędu w okienku graficznym.

2. Rozwiąż równanie


Eksperymentuj z różnymi sposobami implementacji macierzy (klasycznie i powłokowo).

Praca z PETSc

Kompilowanie programów

hydra:/usr/home/bin> make moj_program

Aby jednak to działało, należy jednak napisać własny plik tekstowy nazwany Makefile w którym podane zostaną (ale tylko raz) wszystkie parametry potrzebne do kompilowania i linkowania programu. Przykładowy plik Makefile, pozwalający na skompilowanie programu z dołączeniem bibliotek PETSc podajemy poniżej. Zmienna BOPT mówi jaka wersja programu ma być tworzona. BOPT=O oznacza program zoptymalizowany, BOPT=g oznacza wersję do odpluskwiania (debuggingu). Ważne jest, żeby gotowy (tzn. odpluskwiony) program kompilować z opcją BOPT=O, gdyż to daje kilkukrotnie mniejszy (około 5 razy) i szybszy kod wynikowy. Oczywiście, aby w ogóle dało się skompilować program, muszą być ustawione zmienne środowiskowe opisane w rozdziale "Zaczynamy" na stronie 7. Tworzenie Makefile'ów jest odrębną sztuką. Zamiast ją zgłebiać, proponujemy pisanie własnych przez prostą modyfikację poniższego: 

Makefile

BOPT=O
include $(PETSC_DIR)/bmake/$(PETSC_ARCH)/base
CFLAG          = $(CPPFLAGS) D__SDIR__='"$(LOCDIR)"' $(BS_INCLUDE)
LIBBASE        = libpetscsles
LOCDIR         = /usr/home/students/bojko/source/

moj_program: moj_program.o  
             $(CLINKER) -o moj_program moj_program.o  $(PETSC_LIB)
              $(RM) moj_program.o

Uruchamianie programów

hydra:/usr/home/bin> moj_program [opcje]

Drugi sposób stosujemy, gdy uruchamiamy program na maszynie wieloprocesorowej z zainstalowaną biblioteką MPI. Wówczas program uruchamia się komendą:

hydra:/usr/home/bin> mpirun -np 4 moj_program [opcje]

Opcja -np 4 oznacza liczbę procesorów, na których będzie uruchomiony moj_program (w tym wypadku 4). Dalej podajemy nazwę programu i ewentualne opcje samego programu. 

Co jeszcze trzeba wiedzieć?

#include "sles.h"

Jak już wspomnieliśmy, dzięki użyciu funkcji main() z argumentami argc, args oraz wywołaniu funkcji PetscInitialize(), tekst z linii komend zostanie przekazany bezpośrednio do programu i potraktowany jako opcje, co pozwala na sterowanie wieloma parametrami programu. Można zmieniać rozmiar zadania, podawać dodatkowe parametry itp.

W pełnym wykorzystaniu opcji pomocne będą funkcje: OptionsGetXXX(char* pre, char *name, XXX *zmienna,int *flag) gdzie w miejscu XXX wstawiamy typ wartości podawanej z linii komend: Int, Double, Scalar, String, DoubleArray. Na przykład funkcja

....
OptionsGetInt(PETSC_NULL,"-N",&rozmiar);
....

Argumenty funkcji OptionsGetXXX() mają następujące znaczenie: pierwszy to przedrostek, u nas będzie zawsze ustawiony na PETSC_NULL. Drugi to poszukiwany ciąg znaków, a trzeci argument to wskaźnik zmiennej do której będzie przekazywany wynik. Ostatni argument to wskaźnik do zmiennej, w której zapisane zostanie czy przypisanie wartości miało miejsce, czy nie. Przydatna jest też funkcja OptionsHasName(char* pre, char *name,int *flag), która sprawdza, czy dany ciąg znaków name pojawił się w linii komend i wynik zapisuje w zmiennej flag.

Ważnym ułatwieniem w pisaniu programów jest to, że wszystkie funkcje w PETSc zwracają kody błędów. Jest też makro CHKERRA(int ierr), która w przypadku wystąpienia błędu poda numer linii programu i nazwę pliku z kodem źródłowym oraz krótki opis błędu. Jeżeli zatem każdą funkcję PETSc wywołujemy następująco:

...
ierr = VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,N,&v); CHKERRA(ierr);
ierr = VecSet(&val,v); CHKERRA(ierr);
...

Przykłady

Opcje PETSc.

Opcja -sles_view spowoduje wypisanie na konsolę informacji na temat SLESu

Opcja -vec_view po wywołaniu w programie funkcji VecAssemblyBegin(v) zostanie wypisany na konsolę wektor v. Podobna do niej -vec_view_draw narysuje w oknie graficznym wektor jako funkcję indeksu.

Opcja -mat_view po wywołaniu w programie funkcji MatAssemblyBegin(A,FINAL_ASSEMBLY) zostanie wypisana na konsolę macierz A. Podobna do niej -mat_view_draw narysuje w oknie graficznym strukturę miejsc niezerowych macierzy.

Opcja -draw_pause <n> spowoduje zatrzymanie przeglądarki graficznej (zarówno wywoływanej opcją z linii komend jak i z programu) na n sekund. Jeżeli n=0 to przeglądarka czeka na kliknięcie klawiszem myszki. To bardzo przydatna opcja, gdyż często przeglądarka jest zamykana zaraz po zakończeniu rysowania, co w wielu przypadkach nie wystarcza nawet na zauważenie, że okno pojawiło się na ekranie.

Opcją -ksp_type <typ> możemy zmienić rodzaj metody iteracyjnej używanej do rozwiązywania układu równań (szczegóły w rozdziale 0 na stronie 29) Inne opcje będziemy omawiać na bieżąco.

Opis opcji dostępnych w każdym z programów jest wypisywany gdy uruchamiamy program z opcją help.

Opcje użytkownika.

#include "sles.h"
static char help[]="Pomoc";

int main(int argc,char **args)
{
 int N=5,pc_flag=0;
 double af=0.1;

 PetscInitialize(&argc,&args,PETSC_NULL,help);
 OptionsGetInt(PETSC_NULL,"-N",&N);
 OptionsGetDouble(PETSC_NULL,"-alfa",&af);
 OptionsHasName(PETSC_NULL,"-bez_pc",&pc_flag);
 PetscPrintf(MPI_COMM_WORLD,"rozmiar=%i,af=%d,pc_flag=%i\n",N,af,pc_flag);
 PetscFinalize();

 return(0)
}

hydra:/usr/home/bin/> program -help -N 10 -alfa 0.22

spowoduje przypisanie zmiennej rozmiar wartości 10, zmiennej af wartości 0.22, oraz zostanie wypisana pomoc do pakietu z uwzględnieniem stałej tekstowej help (patrz wyżej).

hydra:/usr/home/bin/> program -N 23 -bez_pc

spowoduje przypisanie zmiennej rozmiar wartości 23, ustawienia pc_flag na TRUE, a zmienna af pozostanie bez zmian, tzn. równa 0.1.

Ćwiczenie

1. Wzbogać swoje dotychczasowe programy o możliwość ustawiania kluczowych parametrów z linii komend.

Szczegóły o preconditionerze AMS, których nie znajdziecie w oficjalnym manualu

Załóżmy, że mamy już wygenerowany obiekt PC (nieważne, czy wydobyty ze SLESu funkcją SLESGetPC(), czy wygenerowany funkcją PCCreate()) i ustawione operatory. Aby ustawić preconditioner Schwarza, należy wywołać funkcję: PCSetType(pc,PCASM). Funkcje służące do sterowania tym preconditionerem pozwalają na automatyzację tworzenia jego struktury. W zasadzie jedyną rzeczą, jaką użytkownik musi sam zaimplementować, jest dekompozycja obszaru.

Funkcje ASM można podzielić na trzy zasadnicze typy:

• Służące do generowania i obsługi dekompozycji: PCASMCreateSubdomains2D(), PCASMSetOverlap().
• Służące do kontroli sposobu działania: PCASMGetSubSLES(), PCASMSetType().
• Służące do kontroli implementacji równoległej PCASMSetLocalSubdomains() i

Zbiory indeksów

...
#define MP MPI_COMM_WORLD
IS is;
Int indeksy[4]={0,5,12,17,22};
...
ISCreateGeneral(MP,5, indeksy,&is);
...

...
#define MP MPI_COMM_WORLD
IS is;
...
ISCreateStride(MP,5,2,3,&is);
...

Dekompozycja

Dekompozycję obszaru podaje się jako tablicę zbiorów indeksów (IS), gdzie każdy zbiór indeksów podaje numery współrzędnych w jednym podobszarze. Przypuśćmy, że mamy obszar L-kształtny. Rysunek 7, pokazuje jak ponumerowane są węzły siatki. Cała funkcja siatkowa na tym obszarze zapisywana jest jako wektor o 48 współrzędnych. Wprowadzamy dekompozycję na trzy podobszary jak na rysunku 5. Dekompozycję w tym przypadku zapisujemy więc jako 3­elementową tablicę zmiennych typu IS. Będą to następujące zbiory:

• is[0] {19,..,23,27,...,31,35,...,39,43,...,47 }
• is[1]  {16,..,20,24,..28,32..,36,40,...,44}
• is[3]  {0,...,19}

Przy podawaniu dekompozycji musimy sami zdecydować, czy zdajemy się na funkcję automatycznie ustawiającą wielkość zakładki, czy zakładkę definiujemy sami i takie zbiory indeksów musimy wygenerować. W powyższym przykładzie dekompozycja została zdefiniowana z zakładkami, bo tak uzyskujemy pełną kontrolę nad geometrią podobszarów. Zbiór indeksów wstawiamy do PC przy pomocy funkcji PCASMSetTotalSubdomains(PC pc, int N, IS *is). Pierwszy argument to zmienna typu PC służąca do kontroli obiektu, drugi to całkowita liczba podobszarów a trzeci to tablica zbiorów indeksów opisująca dekompozycję. Ta funkcja automatycznie rozdysponowuje podobszary pomiędzy procesory. Można też samemu zdecydować ile podobszarów będzie w poszczególnych procesorach przy pomocy funkcji PCASMSetLocalSubdomains(PC pc, int n, IS *is) Pierwszy argument to zmienna typu PC powiązana z obiektem, drugi to liczba podobszarów w danym procesorze, a trzeci to tablica zbiorów indeksów z podobszarami dla tego procesora. Ostatnia zmienna może przyjąć wartość PETSC_NULL, gdy PETSc ma samo zdecydować, które podobszary mają trafić do danego procesora. Gdy powyższe funkcje są wywoływane w programie wykonywanym wielowątkowo, to muszą być wywołane przez wszystkie procesy w obrębie komunikatora MPI, przy czym pierwsza musi być wywołana z tą samą we wszystkich wątkach tablicą zbiorów indeksów.

Dodatkowo autorzy dołączyli do pakietu funkcję PCASMCreateSubdomains2D(int m,int n,int M,int N,int dof,int overlap,int *Nsub,IS **is) która służy do utworzenia dekompozycji prostokątnego obszaru dwuwymiarowego z regularną siatką na M*N prostokątnych podobszarów. Argumenty tej funkcji to po kolei: rozmiar siatki w poziomie, rozmiar siatki w pionie, liczba podobszarów w poziomie, liczba podobszarów w pionie, liczba stopni swobody siatki, szerokość zakładki, wskaźnik do zmiennej, w której znajdzie się całkowita liczba utworzonych podobszarów i ostatni argument to wskaźnik do tablicy zbiorów indeksów, która zostanie wygenerowana przez tę funkcję.

Zakładka

Zakładka generowana automatycznie tworzona jest na podstawie niezerowej struktury macierzy. Konkretne problemy mogą prowadzić do innych struktur zakładki, na przykład funkcja PCASMCreateSubdomains2D() tworzy zakładkę w innym kształcie niż zakładka utworzona automatycznie (Rysunek 9), dlatego dobrze jest samemu zdefiniować dekompozycję wraz z zakładkami.

Wybór typu AMS

PC_ASM_BASIC metoda podstawowa pełna interpolacja i restrykcja

PC_ASM_RESTRICT pełna restrykcja, lokalna interpolacja w procesorze

PC_ASM_INTERPOLATE pełna interpolacja, lokalna restrykcja w procesorze

PC_ASM_NONE lokalna restrykcja i interpolacja w procesorze

Wszystkie te metody związane są ściśle z implementacją równoległą, to znaczy wszelkie obcięcia i interpolacje odnoszą się do danych pochodzących z innych procesorów. Jeżeli jeden procesor ma kilka podobszarów to w obrębie jego danych stosowana jest zawsze metoda podstawowa - i słusznie, bo wszystkie innowacje mają na celu wyeliminowanie zbędnej komunikacji, która często jest kosztowna, stąd w obrębie jednego procesora nie warto stosować tych metod. Wszystkie metody rozwiązują układ bez grubej siatki.

Podsumowanie

1. Deklarujemy zmienną typu PC: PC pc;
2. Wydobywamy ze SLESu obiekt PC funkcją SLESGetPC(sles,&pc)
3. Ustawiamy typ preconditionera na ASM przy pomocy funkcji PCSetType(pc,PCASM)
4. Definiujemy dekompozycję jako zbiór indeksów, można to zrobić na przykład funkcją PCASMCreateSubdomains2D(), lub samodzielnie
5. Wstawiamy dekompozycję do PC funkcją PCASMSetTotalSubdomains(pc,nsub,dekomp), gdzie nsub to liczba podobszarów a dekomp tablica zbiorów indeksów.
6. Ustawiamy zakładkę funkcją PCASMSetOverlap(pc,zakl). Należy pamiętać o tym, że niezerowa wartość zmiennej zakl spowoduje automatyczne wygenerowanie dodatkowej zakładki o tej szerokości. Zatem gdy dekompozycja została podana z zakładkami należy zmienną zakl ustawić na 0.

• W punkcie 2 obiekt PC trzeba samemu wykreować funkcją PCCreate(&pc)
• Po punkcie 6 trzeba samemu wywołać funkcję PCSetUp(pc). Spowoduje to utworzenie zakładek, przygotowanie SLESów wektorów dla podobszarów oraz obiektów przerzucających dane między wektorami (Scatter) dla zadań na podobszarach.
• Preconditioner stosujemy używając funkcji PCApply(PC pc,Vec v0, Vec v1)

Szczegóły

Przykład

#include "sles.h";
PC pc,pc1;

SLES *slesy;
...
PCASMGetSubSLES(pc,&n,&zero,&slesy);
for(i=zero;i<zero+n;i++)
{
 SLESGetPC(slesy[i],&pc1);
 PCSetType(pc1,PCICC);
}

Rysunek 10. Struktura preconditionera Schwarza dla 4 podobszarów.

II. Rozwiązywanie równań nieliniowych

• wygenerować macierz układu i prawą stronę
• utworzyć kontekst SLESu przy pomocy SLESCreate()
• przekazać SLESowi parametry zadania, tzn. macierz i wektor prawej strony: SLESSetOperators()
• ustawić pożądane parametry SLESu, np. rodzaj metody iteracyjnej, warunki stopu, itp. SLESSetFromOptions()
• rozwiązać równanie przy pomocy SLESSolve()

Podobnie będzie się nam pracowało z kolejnym składnikiem PETSc, służącym tym razem do (równoległego) rozwiązywania nieliniowych układów równań: SNES. Zanim przejdziemy do omówienia sposobów wykorzystania tego komponentu PETSc, zrobimy najpierw krótki wstęp o metodach rozwiązywania równań nieliniowych. Po przypomnieniu metod rozwiązywania takich równań, przedstawimy ogólny schemat użycia SNESu - nieliniowego analogonu SLESu - obiektu służącego do rozwiązywania równań nieliniowych. Następnie zobaczymy na dwóch przykładach, jak w praktyce wygląda stosowanie SNESu. Między innymi, użyjemy SNESu do zaimplementowania prostego programu rozwiązującego układ powstały po dyskretyzacji nieliniowego zagadnienia konwekcji-dyfuzji

W trakcie szczegółowego omawiania przedstawionych przykładów, poznamy techniki efektywnego wykorzystania całej naszej wiedzy o dotychczas poznanych składnikach PETSc (macierzach, SLESie, itp.) oraz omówimy bliżej bardzo pożyteczną ideę kontekstu.

Zakończymy tę część opisem możliwości modyfikacji działania SNESu: wyboru wariantu metody Newtona, kryteriów stopu, itd. oraz podsumowaniem składni wywołań procedur SNESu.

Pierwszy "poważny" program używający PETSc - rozwiązywanie równania Poissona

przy czym rozważymy przypadek gdy .

Jak wiemy, dyskretyzacja taka prowadzi do następującej postaci macierzowej (patrz [6]):

gdzie macierz A ma postać:

, 

static char help[] = "Rozwiązuje pięciodiagonalny układ z użyciem SLES.\n\n";

#include "sles.h"
#include <stdio.h>

int main(int argc,char **args)
{
  Vec     x, b, u;      
  Mat     A;            /* macierz układu równań */
  SLES    sles;         /* kontekst SLESu */
  int     ierr, i, n = 10, m = 10,col[5], its,flg,k,l;
  Scalar  minus_one = -1.0, one = 1.0, val[5],h;
  double  norm;

  PetscInitialize(&argc,&args,PETSC_NULL,help);
  OptionsGetInt(PETSC_NULL,"n",&n,&flg);
  OptionsGetInt(PETSC_NULL,"m",&m,&flg);

/* Tworzenie wektorów */
  VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,n*m,&x);
  VecDuplicate(x,&b);
  VecDuplicate(x,&u);
/* Wartości wektora prawej strony */
  val[0]=1;
  VecSet(val,b);

/* Tworzenie macierzy laplasjanu na prostokacie mxn */
  MatCreate(MPI_COMM_WORLD,n*m,n*m,&A);
  h=1/(m*n+1);
  val[0] = -1.0/h; val[1] = -1.0/h; val[2] = 4.0/h;

  val[3] = -1.0/h; val[4] = -1.0/h;

  for (i=0; i<n*m; i++ ) 

  {

    col[0]=i+1; col[1]=i-1; col[2]=i;
    col[3]=i+m; col[4]=i-m;
    l=0;k=5;
    if(i<m) k=4;
    if((i+1)>(n-1)*m){k=4;col[3]=i-m;}
    if((i%m)==0){l=1;k=k-1;col[1]=i+1;}
    if((i+1)%m==0)if(i!=0){l=1;k=k-1;}
    MatSetValues(A,1,&i,k,&col[l],&val[l],INSERT_VALUES);
  }
  MatSetValues(A,1,&i,k,&col[l],&val[l],INSERT_VALUES);
  MatAssemblyBegin(A,MAT_FINAL_ASSEMBLY);
  MatAssemblyEnd(A,MAT_FINAL_ASSEMBLY);

/* Tworzenie kontekstu SLES */
  SLESCreate(MPI_COMM_WORLD,&sles); 

/*Ustawienie operatorów */
  SLESSetOperators(sles,A,A,DIFFERENT_NONZERO_PATTERN); 
  SLESSetFromOptions(sles);

/* rozwiązanie układu liniowego */
  SLESSolve(sles,b,x,&its); 

/* Sprawdzenie błedu */
  VecAXPY(&minus_one,u,x);
  VecNorm(x,NORM_2,&norm);
  PetscPrintf(MPI_COMM_WORLD,"Norma błędu %g, %d iteracji\n",norm,its);
  
/* Zwolnienie przestrzeni roboczej */
  VecDestroy(x);VecDestroy(u);
  VecDestroy(b);MatDestroy(A);
  SLESDestroy(sles);
  PetscFinalize();
  return(0);

}

hydra:/usr/home/students/bojko/> przyklad
Norma błędu 0.00893566, 65 iteracji
hydra:/usr/home/students/bojko/>

KSP, czyli iteracyjne metody rozwiązywania równań

Rysunek 3. Powiązania SLESu z innymi obiektami PETSc.

Jeżeli chcemy wybrać metodę z poziomu kodu źródłowego, trzeba to zrobić w następujący sposób: zadeklarować zmienną typu KSP i powiązać ją z obiektem KSP ze SLESu funkcją SLESGetKSP(SLES sles,KSP *ksp), a potem użyć funkcji KSPSetType(KSP ksp, KSPType itmethod). Zmienna sles jest związana z obiektem SLES, z którego wydobywamy obiekt KSP, z kolei *ksp to wskaźniki do obiektu KSP. itmethod jest stałą PETSc oznaczającą rodzaj metody. Spis stałych znajduje się w tabelce poniżej. Jeżeli po ustawieniu rodzaju metody z poziomu kodu źródłowego funkcją KSPSetType() wywołamy funkcję SLESSetFromOptions() to dodatkowo będziemy w stanie zmienić metodę opcją z linii komend, ale domyślną metodą będzie metoda ustawiona z poziomu kodu źródłowego.

Można też wybrać metodę uruchamiając program z opcją -ksp_type <metoda>. Poniższa tabelka podaje wszystkie stałe, predefiniowane w PETSc i opcje, którymi wybieramy metodę z linii komend

Podsumowanie

• W linii komend przy uruchamianiu programu podać opcję -ksp_type <typ> (patrz tabelka powyżej). Należy pamiętać o wywołaniu w programie funkcji SLESSetFromOptions().

• zadeklarować zmienną typu KSP
• wydobyć funkcją SLESGetKSP() z obiektu typu SLES obiekt KSP wiążąc go z uprzednio zadeklarowaną zmienną typu KSP
• ustawić metodę iteracyjną funkcją KSPSetType()

Przykład

#include "sles.h"

int main(int argc,char **args)
{
 Vec x,b;
 SLES sles;
 KSP  ksp;
 int its;

/* inicjalizacja */
 PetscInitialize(&argc,&args,PETSC_NULL,PETSC_NULL);
 SLESCreate(MPI_COMM_WORLD,&sles);

/* wybór metody KSP */
 SLESGetKSP(sles,&ksp);
 KSPSetType(ksp,KSPRICHARDSON);

 /* W tej części programu muszą zostać ustawone wszystkie parametry SLESu, */
 /* omówione w poprzednich rozdziałach. Dla większej przejrzystości        */
 /* przykładu zostały pominięte                                            */

 SLESSetFromOptions(sles);
 SLESSolve(sles,x,b,&its);

/* zakończenie */
 SLESDestroy(sles);
 PetscFinalize();
}

Warunek stopu

• 
• 
• (w tym przypadku stwierdzona zostaje rozbieżność)
• przekroczono zadaną liczbę iteracji maxits.

KSPSetTolerances(KSP ksp,double rtol,double atol,double dtol,int maxits).

rtol = 10^-5, atol = 10^-50, dtol = 10⁵ i maxits = 10⁵.

Inne przydatne opcje dla KSP to -ksp_monitor i -ksp_xmonitor, które na bieżąco śledzą (odpowiednio: w trybie tekstowym lub graficznym) przebieg procesu iteracyjnego rozwiązywania równania. W pierwszym przypadku na każdym kroku zostaje wypisana na konsolę norma wektora residualnego. W drugim przypadku przebieg zbieżności obserwujemy w oknie graficznym.

Rysunek 4: Przebieg zbieżności dla metody Richardsona. Zauważ, że metoda GMRES (obok) jest znacznie szybsza!	Rysunek 5 Przebieg zbieżności procesu iteracyjnego dl a metody GMRES

Warto wiedzieć, że ...

Po wywołaniu funkcji SLESSolve() należy wywołać funkcję KSPComputeExtremeSingularValues(KSP ksp, double *emax, double *emin), która podaje najmniejszą i największą wartość własną operatora użytego w konkretnej metodzie iteracyjnej.

KSP ksp;
double emax,emin;
...
SLESGetKSP(sles,&ksp);
KSPSetMethod(ksp,KSPCG);
KSPSetComputeSingularValues(ksp);
SLESSolve(sles);
KSPComputeExtremeSingularValues(ksp,&emax,&emin);
PetscPrintf(MPI_COMM_WORLD,"Uwarunkowanie operatora wynosi %d\n",emax/emin);
...

Rysunek 6 Wynik działania opcji -ksp_plot_eigenvalues.

Można także wykorzystać opcję PETSc -ksp_plot_eigenvalues, która powinna wyświetlić wyliczony w/w metodami przybliżony rozkład wartości własnych macierzy naszego układu.

Ćwiczenia

1. Porównaj swoją metodę Richardsona z zaimplementowaną w PETSc.
2. Używając -ksp_type <typ> i -ksp_xmonitor, zobacz, która z dostępnych metod iteracyjnych najszybciej rozwiązuje jednowymiarowe zagadnienie Poissona.
3. Zbadaj, jak parametry zbieżności rtol i atol wpływają na liczbę iteracji i błąd rozwiązania.
4. Użyj KSPComputeEigenvalues() dla oszacowania uwarunkowania macierzy 1-wymiarowego laplasjanu. Porównaj wynik z prawdziwymi wartościami.

PC, czyli preconditionery

polega na zastąpieniu tego układu równoważnym, mnożąc układ wyjściowy przez odwrotność pewnej macierzy B, zwanej preconditionerem:

.

Jeżeli teraz zaczniemy rozwiązywać powyższy układ metodą iteracyjną, np. metodą iteracji prostej to otrzymujemy następujące wzory na kolejne przybliżenia rozwiązania:

.

Oznaczając  mamy:

,

czyli w każdym kroku iteracyjnym mnożymy wektor residualny przez odwrotność macierzy B: po prostu rozwiązujemy układ z macierzą preconditionera. Od macierzy B żądamy:

• po pierwsze, aby łatwo się odwracała (to znaczy, żeby koszt rozwiązania układu z macierzą B był istotnie niższy od kosztu rozwiązania wyjściowego układu z macierzą A) - żeby łatwo było obliczać poprawkę B^-1r_k ;
• po drugie, aby macierz B^-1A miała istotnie niższy współczynnik uwarunkowania niż sama macierz : jak wiadomo, prędkość zbieżności metod iteracyjnych zazwyczaj silnie zależy do współczynnika uwarunkowania macierzy układu; zmniejszenie tego współczynnika poważnie wpływa na obniżenie liczby iteracji i tym samym - kosztu rozwiązania całego układu równań; szczegóły można znaleźć w [6].

Do kontroli preconditionera służy obiekt typu PC, który jest częścią obiektu KSP. Intuicyjnie wydaje się to oczywiste: konkretna metoda iteracyjna praktycznie zawsze musi być stosowana z preconditionerem, na przykład możemy wybrać metodę sprzężonych gradientów z preconditionerem Schwarza. W tym rozdziale zostaną omówione podstawowe zasady korzystania z PC, następnie typy preconditionerów zawarte w pakiecie oraz, dokładnie, metoda tworzenia własnych preconditionerów.

W świetle tego co przed chwilą stwierdziliśmy, każdy utworzony obiekt typu SLES zawiera już obiekt PC. Aby uzyskać do niego bezpośredni dostęp należy skojarzyć go ze zmienną typu PC przy pomocy funkcji SLESGetPC(SLES sles,PC *pc);

SLES sles;
PC pc;
...
SLESCreate(MPI_COMM_WORLD,&sles);
SLESGetPC(sles,&pc);
...

Najczęściej wykorzystywaną operacją na PC jest PCSetType(PC pc,PCType type) - funkcja ustawiająca typ preconditionera. Pierwszy argument to obiekt PC dla którego ustawiamy typ, drugim jest jeden z predefiniowanych typów:

SLES sles;
KSP ksp;
PC pc;
...
SLESCreate(MPI_COM_WORLD,&sles);
...
SLESGetKSP(sles,&ksp);
KSPSetType(ksp,KSPPREONLY);
SLESGetPC(sles,&pc); 
PCSetType(pc,LU);
...
SLESSolve(sles);

...
SLESCreate(MPI_COMM_WORLD,&sles);
SLESGetPC(sles,&pc);
PCSetType(pc,PCICC);
...

Podsumowanie

• W linii komend przy uruchamianiu programu podać opcję -pc_type <typ>. Należy pamiętać o wywołaniu funkcji SLESSetFromOptions().

• zadeklarować zmienną typu PC
• wydobyć ze SLESu obiekt typu PC funkcją SLESGetPC()
• ustawić preconditioner funkcją PCSetType()

Tworzenie własnych preconditionerów

Tak więc, aby wstawić do SLESu własny preconditioner należy:

• zadeklarować zmienną typu PC
• zdefiniować funkcję działającą preconditionerem na wektor residualny (proszę zwrócić uwagę, że preconditioner działa analogicznie jak macierz typu powłokowego)
• wydobyć funkcją SLESGetPC() z obiektu typu SLES obiekt PC wiążąc go z uprzednio zadeklarowaną zmienną typu PC
• ustawić preconditioner na powłokowy (PCSHELL) funkcją PCSetType()
• przekazać do preconditionera funkcję realizującą jego działanie na wektor residualny: PCShellSetApply()

Przykłady

Przykład trywialny

przyklad8_1.c

#include "common.h"
static char help[] ="Preconditioner trywialny\n";

/*************************************************
        Działanie preconditionera
*************************************************/

int Pierwszy_pc(void *ctx,Vec v0,Vec v1)
{
 VecCopy(v0,v1);
 return(0);
}

/*************************************************
            Program glowny
*************************************************/

int main(int argc,char **args)
{
 PetscInitialize(&argc,&args,PETSC_NULL,help);
 Przygotuj_zadanie(N,&sles,&A,&u0,&u,&f);

/*ustawienie preconditionera powłokowego */
 SLESGetPC(sles,&pc);
 PCSetType(pc,PCSHELL);
 PCShellSetApply(pc,Pierwszy_pc,PETSC_NULL);
 PCShellSetName(pc,"Mój pierwszy preconditioner");

/*rozwiązanie zadania */
 Rozwiaz(sles);

/*Zwalnianie pamięci*/
 Zwolnij_pamiec(sles,A,u,u0,f);
 PetscFinalize();
}

hydra:/usr/home/bin/> przyklad
Iteracje = 351
 Blad    = 6.364062e-04

hydra:/usr/home/bin/>

Aby zobaczyć efekt PCShellSetName() trzeba uruchomić program z opcją -sles_view. Oczywiście trywialny preconditioner ma trywialną postać macierzową macierz  jest w tym wypadku macierzą identyczności.

Preconditioner Richardsona.

,

dla odpowiednio dobranej wartości parametru . Jak wiadomo, najlepszy parametr metody Richardsona uzyskuje się, korzystając z najmniejszej i największej wartości własnej macierzy (opis metody Richardsona można znaleźć w [6]). Dlatego jako kontekst podane zostaje oszacowanie na spektrum macierzy. Podobnie jak w poprzednim przypadku, pliki common.h i common.c są podane w przykładzie podsumowującym na stronie 37.

przyklad8_2.c

#include "common.h"
static char help[] ="Preconditioner Richardsona\n";

/***************************************************
          Kontekst dla preconditionera
***************************************************/

typedef struct {
   double lambdamin;
double lambdamax;} Kontekst;

Kontekst k_pc;

/***************************************************
          Dzialanie preconditionera
***************************************************/

int Richardson_pc(void *ctx,Vec v0,Vec v1)
{
 Scalar val=1;
 Kontekst *kn=(Kontekst*)ctx;
 val=2/(kn->lambdamin+kn->lambdamax);
 VecCopy(v0,v1);
 VecScale(&val,v1);
 return(0);
}

/**************************************************
          Program glowny
**************************************************/

main(int argc,char **args)
{
 PetscInitialize(&argc,&args,PETSC_NULL,help);
 Przygotuj_zadanie(N,&sles,&A,&u0,&u,&f);
 SLESGetPC(sles,&pc);
 PCSetType(pc,PCSHELL);
 PCShellSetApply(pc,Richardson_pc,(void*)&k_pc);
 PCShellSetName(pc,"Preconditioner Richardsona");
 k_pc.lambdamin=1/N;
 k_pc.lambdamax=1;
 Rozwiaz(sles); 
 Zwolnij_pamiec(sles,A,u0,u,f);
 PetscFinalize();
}

hydra:/usr/home/bin/> przyklad
Iteracje = 80
 Blad    = 4.366761e-04

hydra:/usr/home/bin/>

Preconditioner Jacobi'ego.

gdzie a_ii oznaczają elementy diagonalne macierzy zadania A. W implementacji tego preconditionera skorzystamy więc ze zmiennej kontekstowej: jako kontekst podamy główną diagonalę macierzy zadania. Zwróćmy uwagę na funkcję PrzygotujPreconditioner() - wykonuje on podobną pracę, co w standardowym przypadku funkcja PCSetUp().

przyklad8_3.c

#include "common.h"
static char help[] ="Preconditioner Jacobi'ego";

/***********************************************
    Inicjalizacja kontekstu preconditionera
***********************************************/

int PrzygotujPreconditioner(Mat A,Vec *k_pc)
{
 int m,n;
 MatGetSize(A,&m,&n);
 If(m!=n)
 {
  PetscPrintf(MPI_COMM_WORLD,"Hej!! Macierz nie jest kwadratowa\n");
 }
 VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,m,k_pc);
 MatGetDiagonal(A,(*k_pc));
 return(0);
}
/***********************************************
          Dzialanie preconditionera
***********************************************/

int wlasny_pc(void *ctx,Vec v0,Vec v1)
{
 Vec *k_pc=(Vec*)ctx;
/* Dzialanie preconditionerem Jacobiego */
 VecPointwiseDivide(v0,*k_pc,v1);
 return(0);
}

/***********************************************
              Program glowny 
***********************************************/

int main(int argc,char **args)
{
 Vec diag;

 PetscInitialize(&argc,&args,PETSC_NULL,help);
 Przygotuj_zadanie(N,&sles,&A,&u0,&u,&f);
 SLESGetPC(sles,&pc);
 PCSetType(pc,PCSHELL);
 PrzygotujPreconditioner(A,&diag);
 PCShellSetApply(pc,wlasny_pc,&diag);
 PCShellSetName(pc,"Preconditioner Jacobi'ego");
 Rozwiaz(sles);
 PetscFinalize();
}

hydra:/usr/home/bin/> przyklad
Iteracje = 63
 Blad    = 4.364761e-04

hydra:/usr/home/bin/>

Przykład podsumowujący: addytywna metoda Schwarza z grubą siatką

przyklad8_4.c

#include "common.h"
static char help[] ="Addytywny preconditioner Schwarza z grubą siatką
                                 Marcin Bojko";

/* Tutaj definiujemy strukture, która bedzie kontekstem preconditionera */
typedef struct {
 Mat I,Ag;               /* macierz interpolacji i zadania na grubej siatce */
 int rozmiar,mg;         /* mg to rozmiar grubej siatki*/
 int m,M,zakl;           /* M to ilość podobszarów w jednym kierunku */
                         /* wszystkich podobszarów będzie M*M */
 IS *boxy;               /* tu będzie składowana dekompozycja */
 Vec fg,ug;              /* pomocnicze wektory zadania na grubej siatce */
 Scalar value[3],val;
 SLES slesg;             /* SLES dla zadania na gubej siatce */
 PC pc_box;              /* preconditioner Schwarza na boxach */
} asm_ctx;
 
int Preconditioner(void *pointer,Vec u0,Vec u1);

void Przygotuj_macierz_interpolacji(asm_ctx *ctx)
{
 int i,j,row,col,r,k,l;
 int mg=ctx->mg,m=ctx->m,rozmiar=ctx->rozmiar;
  
 Scalar val;
 MatCreate(MPI_COMM_WORLD,rozmiar*rozmiar,mg*mg,&ctx->I);
 for(j=0;j<mg;j++)
 for(i=0;i<mg;i++)
 {
  col=i+mg*j;
  row=r=(m-1)*rozmiar+m-1+i*m+j*m*rozmiar;
  val=1;
  MatSetValues(ctx->I,1,&row,1,&col,&val,INSERT_VALUES);
  for(k=1;k<m;k++)
  {
   val=(Scalar)(m-k)/m;
   for(l=0;l<6*k;l++)
   {
    if((l>1)&&(l<k))row=r-k*rozmiar+l;
    if((l>k-1)&&(l<2*k))row=r-k*rozmiar+k+(l-k)*rozmiar;
    if((l>2*k-1)&&(l<3*k))row=r+k+(l-2*k)*(rozmiar-11);
    if((l>3*k-1)&&(l<4*k))row=r+k*rozmiar-(l-3*k);
    if((l>4*k-1)&&(l<5*k))row=r+k*(rozmiar-1)-(l-4*k)*rozmiar;
    if((l>5*k-1)&&(l<6*k))row=r-k-(l-5*k)*(rozmiar-1);
    MatSetValues(ctx->I,1,&row,1,&col,&val,INSERT_VALUES);
   }    
  }
 }
 MatAssemblyBegin(ctx->I,MAT_FINAL_ASSEMBLY);
 MatAssemblyEnd(ctx->I,MAT_FINAL_ASSEMBLY); 
 MatCompress(ctx->I); 
}

Przygotuj_preconditioner(asm_ctx *ctx,PC *pc_shell)
{
 int flag;
 int rozmiar=ctx->rozmiar,M=ctx->M;
 int zakl=ctx->zakl,mg=ctx->mg;
 PC pcg;
 KSP ksp;

 /*Przygotowanie preconditionera Schwarza */
 PCCreate(MPI_COMM_WORLD,&ctx->pc_box);
 PCSetType(ctx->pc_box,PCASM);
 PCASMCreateSubdomains2D(rozmiar,rozmiar,M,M,1,zakl,&i,&ctx->boxy);
 PCASMSetLocalSubdomains(ctx->pc_box,i,ctx->boxy);
 PCSetOperators(ctx->pc_box,A,A,SAME_PRECONDITIONER);
 PCSetVector(ctx->pc_box,u);
 PCASMSetOverlap(ctx->pc_box,0);
 PCSetUp(ctx->pc_box);

 /* gruba siatka */ 
 VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,mg*mg,&ctx->fg);
 VecDuplicate(ctx->fg,&ctx->ug);
 Przygotuj_macierz_laplasjanu(&ctx->Ag,mg,mg);
 SLESCreate(MPI_COMM_WORLD,&ctx->slesg); 
 SLESSetOperators(ctx->slesg,ctx->Ag,ctx->Ag,SAME_PRECONDITIONER);
 SLESGetPC(ctx->slesg,&pcg);
 PCSetType(pcg,PCLU);
 SLESGetKSP(ctx->slesg,&ksp);
 KSPSetType(ksp,KSPPREONLY);
 Przygotuj_macierz_interpolacji(ctx);
}

int main(int argc,char **args)
{
 KSP ksp;
 PC pc_shell;
 asm_ctx ams;
 double norma,emin,emax;
 int i,flag;
 PetscInitialize(&argc,&args,PETSC_NULL,help);
 ams.M=4;
 ams.mg=7;
 ams.zakl=1;
 ams.m=8;
 OptionsGetInt(PETSC_NULL,"M",&ams.M,&flag);
 OptionsGetInt(PETSC_NULL,"mg",&ams.mg,&flag); 
 OptionsGetInt(PETSC_NULL,"m",&ams.m,&flag); 
 OptionsGetInt(PETSC_NULL,"zakl",&ams.zakl,&flag); 
 ams.rozmiar=(ams.mg+1)*ams.m-1;

 Przygotuj_zadanie(ams.rozmiar,&sles,&A,&u0,&u,&f);
 SLESGetKSP(sles,&ksp);
 SLESGetPC(sles,&pc_shell);
 Przygotuj_preconditioner(&ams,&pc_shell);
 PCSetType(pc_shell,PCSHELL);
 PCShellSetApply(pc_shell,Preconditioner,&ams);
 PCShellSetName(pc_shell,"asmbox");
 KSPSetType(ksp,KSPGMRES);
 KSPSetComputeSingularValues(ksp); 

 SLESSetFromOptions(sles); 
 Rozwiaz(sles);
 KSPComputeExtremeSingularValues(ksp,&emax,&emin);
 PetscFPrintf(MPI_COMM_WORLD,stderr," Uwarunkowanie  = %e\n\n",emax/emin);

 SLESDestroy(ams.slesg);
 MatDestroy(ams.Ag);
 VecDestroy(ams.ug);
 VecDestroy(ams.fg);
 MatDestroy(ams.I);
 Zwolnij_pamiec(sles,A,u0,u,f);
 PetscFinalize();
}

int Preconditioner(void *pointer,Vec v0 ,Vec v1)
{
 asm_ctx *ams=(asm_ctx*)pointer;
 int its;
 /*rozwiązanie na boxach */
 PCApply(ams->pc_box,v0,v1);
 /* rozwiazanie na grubej siatce */
 MatMultTrans(ams->I,v0,ams->fg);
 SLESSolve(ams->slesg,ams->fg,ams->ug,&its);
 VecScale(&val,ams->ug);
 MatMultAdd(ams->I,ams->ug,v1,v1);
 return(0);
}

hydra:/usr/home/bin/> przyklad8_4 Liczba iteracji = 24 Blad = 6.442081e-04 Uwarunkowanie = 5.804242e+01 hydra:/usr/home/bin/>

Poniżej przytaczamy pliki źródłowe common.c i common.h, z których korzystaliśmy w niniejszym rozdziale.

common.h

#include "sles.h"
Vec u,u0,f;
Mat A;
SLES sles;
PC pc;
int N=100,its,i;
Scalar val;
double norma;

int Rozwiaz(SLES sles);
int Przygotuj_zadanie(int rozmiar,SLES *sles,Mat *A,Vec *u0,Vec *u,Vec *f);
int Zwolnij_pamiec(SLES sles,Mat A,Vec u0,Vec u,Vec f);
int Przygotuj_macierz_laplasjanu(Mat *A,int roz_x,int roz_y);



common.c

#include "common.h"
int Przygotuj_macierz_laplasjanu(Mat *A,int roz_x,int roz_y)
{ 
 Scalar val;
 int n,m,i,j;
 n=roz_x*roz_y;
 MatCreateSeqAIJ(MPI_COMM_WORLD,n,n,5,PETSC_NULL,A);;
 for(i=0;i<n;i++)
 {
  val=4;
  MatSetValues(*A,1,&i,1,&i,&val,INSERT_VALUES);;
     /* elementy na dalekich kodiagonalach */
  val=-1;
  j=i+roz_y;
  if(j<n)
  {
   MatSetValues(*A,1,&i,1,&j,&val,INSERT_VALUES);;
   MatSetValues(*A,1,&j,1,&i,&val,INSERT_VALUES);;
  }
    /* elementy na bliskich kodiagonalach */
  j=i+1;
  val=-1;
  if(j<n)if(((i+1)%roz_x)!=0||(i==0))
  {
   MatSetValues(*A,1,&i,1,&j,&val,INSERT_VALUES);;
   MatSetValues(*A,1,&j,1,&i,&val,INSERT_VALUES);;
  }
 }
 MatAssemblyBegin(*A,MAT_FINAL_ASSEMBLY); ;
 MatAssemblyEnd(*A,MAT_FINAL_ASSEMBLY); ;
 MatCompress(*A);
 return(0);
}

/*Przygotowanie zadania testowego */
int Przygotuj_zadanie_testowe(int N,SLES *sles,Mat *A,Vec *u0,Vec *u,Vec *f)
{
 PetscRandom rctx;
 VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,N*N,f);
 VecDuplicate(*f,u);
 VecDuplicate(*f,u0);
 Przygotuj_macierz_laplasjanu(A,N,N); 
 SLESCreate(MPI_COMM_WORLD,sles); 
 SLESSetOperators(*sles,*A,*A,SAME_PRECONDITIONER);
 PetscRandomCreate(MPI_COMM_WORLD,RANDOM_DEFAULT,&rctx); 
 VecSetRandom(rctx,*u0); 
 PetscRandomDestroy(rctx); 
 MatMult(*A,*u0,*f);
 return(0);
}

/* Zwolnienie pamięci po zadaniu testowym */
int Zniszcz_zadanie_testowe(SLES sles,Mat A,Vec u0,Vec u,Vec f)
{
 SLESDestroy(sles);
 VecDestroy(u0);
 VecDestroy(u); 
 VecDestroy(f); 
 MatDestroy(A);
}
int Rozwiarz(SLES sles)
{
 SLESSetFromOptions(sles);
 SLESSolve(sles,f,u,&its);

/*Podanie wynikow*/
 val=-1;
 VecAXPY(&val,u,u0);
 VecNorm(u0,NORM_2,&norma);  
 PetscFPrintf(MPI_COMM_WORLD,stderr,"\nLiczba iteracji = %i\n",its); 
 PetscFPrintf(MPI_COMM_WORLD,stderr," Blad           = %e\n",(double)norma);

}

makefile (do skompilowania powyższych przykładów)

BOPT=O
include $(PETSC_DIR)/bmake/$(PETSC_ARCH)/base
CFLAG          = $(CPPFLAGS) D__SDIR__='"$(LOCDIR)"' $(BS_INCLUDE)
LIBBASE        = libpetscsles
LOCDIR         = /home/students/bojko/source/

wszystko: przykład8_1 przykład8_2 przykład8_3 przykład8_4

przykład8_1: przyklad8_1.o  
             $(CLINKER) -o przyklad8_1 przyklad8_1.o  common.o        
                   $(PETSC_LIB)
             $(RM) przyklad8_1.o
przyklad8_2: przyklad8_2.o  
             $(CLINKER) -o przyklad8_2 przyklad8_2.o common.o        
                  $(PETSC_LIB)
              $(RM) przyklad8_2.o

przyklad8_3: przyklad8_3.o  
             $(CLINKER) -o przyklad8_3 przyklad8_3.o common.o        
                   $(PETSC_LIB)
              $(RM) przyklad8_3.o

przyklad8_4: przyklad8_4.o  
             $(CLINKER) -o przyklad8_4 przyklad8_4.o common.o        
                   $(PETSC_LIB)
              $(RM) przyklad8_4.o

hydra:/usr/home/students/bojko/>make przyklad8_1

Plik wykonywalny otrzyma nazwę przyklad8_1, więc będziemy go uruchamiać, pisząc

hydra:/usr/home/students/bojko/>przyklad8_1

Można też od razu skompilować wszystkie programy (pod warunkiem, że wszystkie pliku źródłowe są w jednym katalogu) poleceniem:

hydra:/usr/home/students/bojko/>make wszystko

Szczegóły o preconditionerze AMS, których nie znajdziecie w oficjalnym manualu

Załóżmy, że mamy już wygenerowany obiekt PC (nieważne, czy wydobyty ze SLESu funkcją SLESGetPC(), czy wygenerowany funkcją PCCreate()) i ustawione operatory. Aby ustawić preconditioner Schwarza, należy wywołać funkcję: PCSetType(pc,PCASM). Funkcje służące do sterowania tym preconditionerem pozwalają na automatyzację tworzenia jego struktury. W zasadzie jedyną rzeczą, jaką użytkownik musi sam zaimplementować, jest dekompozycja obszaru.

Funkcje ASM można podzielić na trzy zasadnicze typy:

• Służące do generowania i obsługi dekompozycji: PCASMCreateSubdomains2D(), PCASMSetOverlap().
• Służące do kontroli sposobu działania: PCASMGetSubSLES(), PCASMSetType().
• Służące do kontroli implementacji równoległej PCASMSetLocalSubdomains() i

Zbiory indeksów

...
#define MP MPI_COMM_WORLD
IS is;
Int indeksy[4]={0,5,12,17,22};
...
ISCreateGeneral(MP,5, indeksy,&is);
...

...
#define MP MPI_COMM_WORLD
IS is;
...
ISCreateStride(MP,5,2,3,&is);
...

Dekompozycja

Dekompozycję obszaru podaje się jako tablicę zbiorów indeksów (IS), gdzie każdy zbiór indeksów podaje numery współrzędnych w jednym podobszarze. Przypuśćmy, że mamy obszar L-kształtny. Rysunek 7, pokazuje jak ponumerowane są węzły siatki. Cała funkcja siatkowa na tym obszarze zapisywana jest jako wektor o 48 współrzędnych. Wprowadzamy dekompozycję na trzy podobszary jak na rysunku 5. Dekompozycję w tym przypadku zapisujemy więc jako 3­elementową tablicę zmiennych typu IS. Będą to następujące zbiory:

• is[0] {19,..,23,27,...,31,35,...,39,43,...,47 }
• is[1]  {16,..,20,24,..28,32..,36,40,...,44}
• is[3]  {0,...,19}

Przy podawaniu dekompozycji musimy sami zdecydować, czy zdajemy się na funkcję automatycznie ustawiającą wielkość zakładki, czy zakładkę definiujemy sami i takie zbiory indeksów musimy wygenerować. W powyższym przykładzie dekompozycja została zdefiniowana z zakładkami, bo tak uzyskujemy pełną kontrolę nad geometrią podobszarów. Zbiór indeksów wstawiamy do PC przy pomocy funkcji PCASMSetTotalSubdomains(PC pc, int N, IS *is). Pierwszy argument to zmienna typu PC służąca do kontroli obiektu, drugi to całkowita liczba podobszarów a trzeci to tablica zbiorów indeksów opisująca dekompozycję. Ta funkcja automatycznie rozdysponowuje podobszary pomiędzy procesory. Można też samemu zdecydować ile podobszarów będzie w poszczególnych procesorach przy pomocy funkcji PCASMSetLocalSubdomains(PC pc, int n, IS *is) Pierwszy argument to zmienna typu PC powiązana z obiektem, drugi to liczba podobszarów w danym procesorze, a trzeci to tablica zbiorów indeksów z podobszarami dla tego procesora. Ostatnia zmienna może przyjąć wartość PETSC_NULL, gdy PETSc ma samo zdecydować, które podobszary mają trafić do danego procesora. Gdy powyższe funkcje są wywoływane w programie wykonywanym wielowątkowo, to muszą być wywołane przez wszystkie procesy w obrębie komunikatora MPI, przy czym pierwsza musi być wywołana z tą samą we wszystkich wątkach tablicą zbiorów indeksów.

Dodatkowo autorzy dołączyli do pakietu funkcję PCASMCreateSubdomains2D(int m,int n,int M,int N,int dof,int overlap,int *Nsub,IS **is) która służy do utworzenia dekompozycji prostokątnego obszaru dwuwymiarowego z regularną siatką na M*N prostokątnych podobszarów. Argumenty tej funkcji to po kolei: rozmiar siatki w poziomie, rozmiar siatki w pionie, liczba podobszarów w poziomie, liczba podobszarów w pionie, liczba stopni swobody siatki, szerokość zakładki, wskaźnik do zmiennej, w której znajdzie się całkowita liczba utworzonych podobszarów i ostatni argument to wskaźnik do tablicy zbiorów indeksów, która zostanie wygenerowana przez tę funkcję.

Zakładka

Zakładka generowana automatycznie tworzona jest na podstawie niezerowej struktury macierzy. Konkretne problemy mogą prowadzić do innych struktur zakładki, na przykład funkcja PCASMCreateSubdomains2D() tworzy zakładkę w innym kształcie niż zakładka utworzona automatycznie (Rysunek 9), dlatego dobrze jest samemu zdefiniować dekompozycję wraz z zakładkami.

Wybór typu AMS

PC_ASM_BASIC metoda podstawowa pełna interpolacja i restrykcja

PC_ASM_RESTRICT pełna restrykcja, lokalna interpolacja w procesorze

PC_ASM_INTERPOLATE pełna interpolacja, lokalna restrykcja w procesorze

PC_ASM_NONE lokalna restrykcja i interpolacja w procesorze

Wszystkie te metody związane są ściśle z implementacją równoległą, to znaczy wszelkie obcięcia i interpolacje odnoszą się do danych pochodzących z innych procesorów. Jeżeli jeden procesor ma kilka podobszarów to w obrębie jego danych stosowana jest zawsze metoda podstawowa - i słusznie, bo wszystkie innowacje mają na celu wyeliminowanie zbędnej komunikacji, która często jest kosztowna, stąd w obrębie jednego procesora nie warto stosować tych metod. Wszystkie metody rozwiązują układ bez grubej siatki.

Podsumowanie

1. Deklarujemy zmienną typu PC: PC pc;
2. Wydobywamy ze SLESu obiekt PC funkcją SLESGetPC(sles,&pc)
3. Ustawiamy typ preconditionera na ASM przy pomocy funkcji PCSetType(pc,PCASM)
4. Definiujemy dekompozycję jako zbiór indeksów, można to zrobić na przykład funkcją PCASMCreateSubdomains2D(), lub samodzielnie
5. Wstawiamy dekompozycję do PC funkcją PCASMSetTotalSubdomains(pc,nsub,dekomp), gdzie nsub to liczba podobszarów a dekomp tablica zbiorów indeksów.
6. Ustawiamy zakładkę funkcją PCASMSetOverlap(pc,zakl). Należy pamiętać o tym, że niezerowa wartość zmiennej zakl spowoduje automatyczne wygenerowanie dodatkowej zakładki o tej szerokości. Zatem gdy dekompozycja została podana z zakładkami należy zmienną zakl ustawić na 0.

• W punkcie 2 obiekt PC trzeba samemu wykreować funkcją PCCreate(&pc)
• Po punkcie 6 trzeba samemu wywołać funkcję PCSetUp(pc). Spowoduje to utworzenie zakładek, przygotowanie SLESów wektorów dla podobszarów oraz obiektów przerzucających dane między wektorami (Scatter) dla zadań na podobszarach.
• Preconditioner stosujemy używając funkcji PCApply(PC pc,Vec v0, Vec v1)

Szczegóły

Przykład

#include "sles.h";
PC pc,pc1;

SLES *slesy;
...
PCASMGetSubSLES(pc,&n,&zero,&slesy);
for(i=zero;i<zero+n;i++)
{
 SLESGetPC(slesy[i],&pc1);
 PCSetType(pc1,PCICC);
}

Rysunek 10. Struktura preconditionera Schwarza dla 4 podobszarów.

II. Rozwiązywanie równań nieliniowych

• wygenerować macierz układu i prawą stronę
• utworzyć kontekst SLESu przy pomocy SLESCreate()
• przekazać SLESowi parametry zadania, tzn. macierz i wektor prawej strony: SLESSetOperators()
• ustawić pożądane parametry SLESu, np. rodzaj metody iteracyjnej, warunki stopu, itp. SLESSetFromOptions()
• rozwiązać równanie przy pomocy SLESSolve()

Podobnie będzie się nam pracowało z kolejnym składnikiem PETSc, służącym tym razem do (równoległego) rozwiązywania nieliniowych układów równań: SNES. Zanim przejdziemy do omówienia sposobów wykorzystania tego komponentu PETSc, zrobimy najpierw krótki wstęp o metodach rozwiązywania równań nieliniowych. Po przypomnieniu metod rozwiązywania takich równań, przedstawimy ogólny schemat użycia SNESu - nieliniowego analogonu SLESu - obiektu służącego do rozwiązywania równań nieliniowych. Następnie zobaczymy na dwóch przykładach, jak w praktyce wygląda stosowanie SNESu. Między innymi, użyjemy SNESu do zaimplementowania prostego programu rozwiązującego układ powstały po dyskretyzacji nieliniowego zagadnienia konwekcji-dyfuzji

W trakcie szczegółowego omawiania przedstawionych przykładów, poznamy techniki efektywnego wykorzystania całej naszej wiedzy o dotychczas poznanych składnikach PETSc (macierzach, SLESie, itp.) oraz omówimy bliżej bardzo pożyteczną ideę kontekstu.

Zakończymy tę część opisem możliwości modyfikacji działania SNESu: wyboru wariantu metody Newtona, kryteriów stopu, itd. oraz podsumowaniem składni wywołań procedur SNESu.

Równania nieliniowe

,

gdzie . Do rozwiązywania równań powyższej postaci używa się metod iteracyjnych, takich jak metoda iteracji prostej Banacha:

,

czy też metoda Newtona

gdzie  jest macierzą pochodnej (zwanej także jakobianem) odwzorowania F w punkcie x_n. Czytelnika zainteresowanego, jakie założenia na funkcję F oraz przybliżenie początkowe x₀ gwarantują zbieżność powyższych procesów iteracyjnych, odsyłamy do podręczników analizy numerycznej [6], [18], oraz licznych monografii, np. [15], [11].

Zauważmy, że w przypadku iteracji Newtona nie ma potrzeby (ani sensu) odwracania macierzy F'(x_n) dla obliczenia x_n+1. Kolejne przybliżenie rozwiązania x* uzyskamy najpierw wyznaczając poprawkę na x_n , rozwiązując względem układ z macierzą jakobianu, a następnie kładąc . Oczywiście, ponieważ macierz pochodnej zmienia się w każdym kroku, rozwiązanie jednego układu liniowego jest dużo tańsze niż najpierw wyznaczenie macierzy odwrotnej, a dopiero potem pomnożenie jej przez wektor F(x_n).

Reasumując, aby znaleźć nowe przybliżenie, musimy skonstruować macierz pochodnej, a następnie rozwiązać układ liniowy z tą macierzą. Jeśli do rozwiązywania tego układu użyjemy metody iteracyjnej (co może być uzasadnione w przypadku, gdy mamy do czynienia z macierzą rzadką dużego rozmiaru), taka metoda będzie wtedy tzw. niedokładną (ang. inexact) metodą Newtona. Możliwe są też inne modyfikacje metody Newtona, o mniejszym koszcie jednego kroku (często właśnie konstrukcja macierzy jakobianu jest zaskakująco kosztownym etapem metody Newtona). W takich przypadkach czasem stosuje się wariant, w którym macierz jakobianu jest uaktualniana dopiero po wykonaniu kilku kroków metody. Innym rozwiązaniem jest aproksymacja macierzy jakobianu przy pomocy różnic skończonych (wielowymiarowy analog metody siecznych). Zainteresowanych przeglądem rozmaitych metod rozwiązywania układów równań nieliniowych odsyłamy do zwięzłej książki [11] oraz do monografii [15].

Solvery nieliniowe dostępne w PETSc dotyczą wyłącznie metod typu Newtona. Nic dziwnego: implementacja metody iteracji (nomen omen) prostej jest co prawda nieskomplikowana, ale jej szybkość zbieżności pozostawia dużo do życzenia. Natomiast metoda Newtona jest zbieżna kwadratowo, a ponieważ w każdym kroku algorytmu musimy rozwiązać układ równań liniowych, będziemy mieli doskonałą okazję wykorzystania pełnej mocy i elastyczności SLESu.

Na niekorzyść algorytmu Newtona zdaje się działać fakt, że wymaga on dobrego przybliżenia początkowego. Na szczęście, tę wadę metody Newtona często można obejść w przypadku dyskretyzacji równań różniczkowych cząstkowych, gdy "dobre'' przybliżenie początkowe można zgadnąć, lub wyliczyć w mniej lub bardziej wyrafinowany sposób. Ponadto, w PETSc zastosowano heurystyczne techniki "globalizujące'' zbieżność metody Newtona. Bazują one na spostrzeżeniu, że w przypadku, gdy startujemy ze złego przybliżenia, poprawka  jest co prawda wektorem skierowanym w dobrym kierunku (tzn. w stronę rozwiązania x*), ale za dużej długości. Taka sytuacja prowadzi do "przestrzelenia'' rozwiązania i w efekcie do niezbieżności całego procesu. Dlatego wprowadza się dodatkową operację poszukiwania optymalnej długości wektora poprawki (tzw. line search methods). Więcej informacji na ten temat znajduje się w [11], rozdział 8.

Schemat użycia SNESu do rozwiązania równania F(x*)=0

Następnie, powołamy do życia maszynkę do rozwiązywania równań nieliniowych (czyli SNES) i przekażemy do niej dane zadania - powiemy jej, co ma być dla niej funkcją F i pochodną F' (po prostu przekażemy jej parametry - analogicznie jak w SLESie, gdzie musieliśmy przekazać SLESowi macierz układu i wektor prawej strony). W końcu, ustawimy dodatkowe parametry SNESu (albo i nie, pamiętając, że wartości domyślne są zazwyczaj rozsądnie dobrane), wygenerujemy przybliżenie początkowe i każemy SNESowi rozwiązać nasze równanie.

Tak więc, schemat wykorzystania SNESu do rozwiązania równania nieliniowego jest następujący:

• zdefiniować funkcję F i jej jakobian F'
• wygenerować SNES: SNESCreate()
• przekazać SNESowi naszą funkcję i jakobian: SNESSetFunction() oraz SNESSetJacobian()
• ustawić opcje w SNESie, SNESSetFromOptions()
• wyliczyć przybliżenie początkowe
• rozwiązać równanie! SNESSolve()

Pierwsze zadanie nieliniowe w PETSc

Problem.

Naturalnie, rozwiązaniem są pary (x,y) postaci  Rozwiązanie polega na znalezieniu zera funkcji

Jej pochodna jest oczywiście zadana macierzą następującej postaci:

Postępując zgodnie ze schematem, w naszym programie najpierw powinniśmy zdefiniować funkcję F oraz macierz pochodnej. Dla większej elegancji, kody źródłowe funkcji i jej pochodnej będziemy trzymać w osobnych plikach. Umówmy się więc, że plik uklad2x2.c będzie zawierać kod źródłowy programu głównego, tzn. funkcję main(), podczas gdy definicja procedury obliczającej F(X) znajdzie się w pliku fun2x2.c, a kod dla jakobianu F´(X) w pliku jac2x2.c. W kolejnych rozdziałach przyjrzymy się dokładnie zawartości tych plików.

Definicja F

fun2x2.c

#include "snes.h" /* plik z definicjami funkcji i obiektow SNES; 
                     zawiera także dyrektywę #include  "sles.h" */

/******************************************************
        Procedura obliczajaca wartosci funkcji F
******************************************************/
int Funkcja(SNES MojSnes,Vec X,Vec F,void *Ctx)
{
  int    ierr;
  Scalar *TablicaX, *TablicaF;

  /* Pobierz wskazniki do tablicy z wspolrzednymi X i F */
  ierr = VecGetArray(X, &TablicaX); CHKERRQ(ierr);
  ierr = VecGetArray(F, &TablicaF); CHKERRQ(ierr);

  /* Oblicz funkcje F */
  TablicaF[0] = TablicaX[0]*TablicaX[0] + TablicaX[1]*TablicaX[1]  1.0;
  TablicaF[1] = TablicaX[0] + TablicaX[1];

  /* Zamknij dostep do wartosci wektorow */
  ierr = VecRestoreArray(X, &TablicaX); CHKERRQ(ierr);
  ierr = VecRestoreArray(F, &TablicaF); CHKERRQ(ierr); 
  return(0);

}

Sama definicja Funkcji() nie jest skomplikowana. Mając dany wektor X (o dwóch współrzędnych), najpierw przygotujemy się do pobrania z niego kolejnych współrzędnych:

ierr = VecGetArray(X, &TablicaX);
CHKERRQ(ierr);

  TablicaF[0] = TablicaX[0]*TablicaX[0] + TablicaX[1]*TablicaX[1]  1.0;
  TablicaF[1] = TablicaX[0] + TablicaX[1];

Na zakończenie musimy pamiętać, aby odblokować wektory X i F komendą VecRestoreArray(). Ta funkcja uaktualnia wektor po dokonanym dostępie do tablicy jego wartości .

Definicja pochodnej F

jac2x2.c

/******************************************************
                 Definicja pochodnej F
******************************************************/

#include "snes.h"
int Jakobian(SNES MojSnes, Vec X, Mat *Jac, 
                Mat *Precond, MatStructure *flag, void *Ctx)
{
  Scalar *x;            /* Wskaznik do wartosci wektora X */
  Scalar A[4];          /* Tu wpiszemy elementy macierzy Jacobiego */
  int ierr;
  int idx[2] = {0,1};

  ierr = VecGetArray(X, &x); CHKERRQ(ierr);

  /* Oblicz elementy jakobianu i wstaw do macierzy Jakobian */
  A[0] = 2.0*x[0]; A[1] = 2.0*x[1]; /* pierwszy wiersz */
  A[2] = 1.0; A[3] = 1.0;           /* drugi wiersz */
  ierr = MatSetValues(*Jac,2,idx,2,idx,A,INSERT_VALUES); CHKERRQ(ierr);
  *flag = SAME_NONZERO_PATTERN;

  /* Odblokuj i uaktualnij X */
  ierr = VecRestoreArray(X,&x); CHKERRQ(ierr);
 
  /* Zloz macierz  */
  ierr = MatAssemblyBegin(*Jac, MAT_FINAL_ASSEMBLY); CHKERRQ(ierr);
  ierr = MatAssemblyEnd(*Jac, MAT_FINAL_ASSEMBLY); CHKERRQ(ierr);

  return(0);
}

int Jakobian(SNES MojSnes, Vec X, Mat *Jac, Mat *Precond, MatStructure *flag, void *Ctx);

gdzie MojSnes jest obiektem SNES do którego zostanie później przekazana ta procedura, a X jest punktem w którym liczymy jakobian. Do macierzy Jac (zwróćmy uwagę, że argumentem jest wskaźnik, a nie sama macierz!) jest wpisywana wyznaczona macierz pochodnej i to jest podstawowe zadanie tej procedury: dostarczenie sposobu obliczania macierzy F'(X).

Macierz Precond oznacza macierz preconditionera (zazwyczaj będzie to ta sama macierz Jac). Parametr flag jest informacją dla PETSc, czy w następnej iteracji Newtona będzie można wykorzystać struktury preconditionera, zbudowane na użytek poprzedniej - podobnie jak w przypadku funkcji SLESSetOperators(). Wartości, jakie można przypisywać parametrowi flag były opisane w poprzedniej części (patrz Rozdział 4 na stronie 22). Ostatni parametr, Ctx, to kontekst definiowany przez użytkownika. Może on zostać wykorzystany do przekazania dodatkowych parametrów z programu potrzebnych do wyliczenia F', podobnie jak w przypadku implementacji funkcji F w procedurze Funkcja(). W naszym przykładzie nie korzystamy z Ctx.

Program główny: rozwiązanie równania przy pomocy SNESu

uklad2x2.c

#include "snes.h"
#include <stdio.h>

static char help[] = "Rozwiazuje nieliniowy uklad 2x2\n\
Opcje: -x0 [Scalar] -y0 [Scalar] wartosci wspolrzednych przybl. poczatk.\n\n";

/* Deklaracje procedur obliczajacych funkcje i jakobian  */
int Jakobian(SNES,Vec,Mat*,Mat*,MatStructure*,void*);
int Funkcja(SNES,Vec,Vec,void*);

/******************************************************
                  Program glowny
******************************************************/
int main( int argc, char **argv )
{
  SNES     MojSnes;        /* obiekt SNES, ktorym rozwiazemy zadanie */
  Vec      X, R;           /* wektor rozwiazania i residualny */
  Mat      MatJ;           /* macierz jakobianu */
  int      ierr, flg, its;
  int      idx[2] = {0,1}; 
  Scalar   X0[2];          /* wspolrz. przyblizenia poczatkowego */
 
  PetscInitialize( &argc, &argv,PETSC_NULL,help );

/* Tworzenie potrzebnych obiektow: SNESu, wektorow, macierzy jakobianu */
  ierr = SNESCreate(MPI_COMM_WORLD,SNES_NONLINEAR_EQUATIONS,&MojSnes); 
  CHKERRA(ierr);
  ierr = VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,2,&X); CHKERRA(ierr);
  ierr = VecDuplicate(X,&R); CHKERRA(ierr);
  ierr = MatCreate(MPI_COMM_WORLD,2,2,&MatJ); CHKERRA(ierr);

/* Przekaz SNESowi funkcje i wektor residualny   */
  ierr = SNESSetFunction(MojSnes, R, Funkcja, PETSC_NULL); CHKERRA(ierr);

/* Przekaz SNESowi macierz jakobianu i funkcje obliczajaca jakobian  */
  ierr = SNESSetJacobian(MojSnes,MatJ,MatJ,Jakobian,PETSC_NULL);CHKERRA(ierr);

/*  Uwzglednij opcje uruchomienia SNESu typu -snes_view -snes_monitor */

  ierr = SNESSetFromOptions(MojSnes); CHKERRA(ierr);

/* Przyblizenie poczatkowe  */

  ierr = OptionsGetScalar( PETSC_NULL, "-x0", &X0[0], &flg ); CHKERRA(ierr);
  if( !flg ) X0[0] = 1.0;
  ierr = OptionsGetScalar( PETSC_NULL, "-y0", &X0[1], &flg ); CHKERRA(ierr);
  if( !flg ) X0[1] = 2.0;
  ierr = VecSetValues(X, 2, idx, X0, INSERT_VALUES ); CHKERRA(ierr);
  ierr = VecAssemblyBegin(X); CHKERRA(ierr);
  ierr = VecAssemblyEnd(X); CHKERRA(ierr);

/* Rozwiaz!    */
  ierr = SNESSolve(MojSnes,X,&its); CHKERRA(ierr);
  
  PetscPrintf(MPI_COMM_WORLD, "Liczba iteracji = %d\n", its);
  PetscPrintf(MPI_COMM_WORLD,"Wektor rozwiazania:\n");
  ierr = VecView(X, VIEWER_STDOUT_WORLD); CHKERRA(ierr);

/* Zwolnij pamiec */
  ierr = VecDestroy(X); CHKERRA(ierr); 
  ierr = VecDestroy(R); CHKERRA(ierr);
  ierr = MatDestroy(MatJ); CHKERRA(ierr); 
  ierr = SNESDestroy(MojSnes); CHKERRA(ierr);

/* Koniec bajki  */
  PetscFinalize();
  return 0;

}

1. uruchamiamy PETSc;
2. tworzone są potrzebne obiekty: SNES, wektory, macierz jakobianu;
3. SNES otrzymuje potrzebne mu obiekty: funkcję i pochodną;
4. wybieramy przybliżenie początkowe;
5. rozwiązujemy równanie przy pomocy SNESSolve();
6. oglądamy wyniki i sprzątamy po sobie.

Oto przykładowy wynik uruchomienia powyższego programu:

11:/home/staff/przykry/Petsc> test
Liczba iteracji = 7
Wektor rozwiazania:
-0.707107
0.707107

Jak widać, algorytm rzeczywiście jest zbieżny do rozwiązania ( = 0.7071...). Zobaczmy teraz, jakie są szczegóły poszczególnych kroków algorytmu. Na początku pliku uklad2x2.c pojawiają się dyrektywy:

#include "snes.h"
#include <stdio.h>

static char help[] = "Rozwiazuje nieliniowy uklad 2x2\n\
Opcje: -x0 [Scalar] -y0 [Scalar] wartosci wspolrzednych przybl. poczatk.\n\n";

int Jakobian(SNES,Vec,Mat*,Mat*,MatStructure*,void*);
int Funkcja(SNES,Vec,Vec,void*);

Na początku funkcji main() deklarujemy kilka zmiennych roboczych:

SNES     MojSnes;        /* obiekt SNES, ktorym rozwiazemy zadanie */
Vec      X, R;           /* wektor rozwiazania i residualny */
Mat      MatJ;           /* macierz jakobianu */
int      ierr, flg, its;
int      idx[2] = {0,1}; 
Scalar   X0[2];          /* wspolrz. przyblizenia poczatkowego */

PetscInitialize( &argc, &argv,PETSC_NULL,help );

SNESCreate(MPI_COMM_WORLD,SNES_NONLINEAR_EQUATIONS,&MojSnes);

VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,2,&X); 
VecDuplicate(X,&R);

MatCreate(MPI_COMM_WORLD,2,2,&MatJ);

Druga funkcja przekazuje do SNESu macierz jakobianu i metodę uaktualniania go: int SNESSetJacobian( SNES MojSnes, Mat Jac, Mat Prec, int (*Jakobian)(SNES, Vec, Mat*, Mat*, MatStructure*,void*), void *Ctx ) Podobnie jak poprzednio, pierwszym argumentem jest MojSnes - obiekt SNESu, do którego chcemy przekazać funkcję obliczającą F'(X), tzn. macierz jakobianu. Drugim argumentem jest więc macierz jakobianu Jac, do której będą wprowadzane wartości elementów, obliczone w procedurze Jakobian(). Trzecim argumentem jest macierz preconditionera Prec dla macierzy Jac, przydatna przy rozwiązywaniu układów z tą macierzą. Zazwyczaj wystarcza podać jako Prec po prostu tą samą macierz Jac. Kolejny, czwarty argument to nazwa procedury - u nas: Jakobian() - obliczającej elementy macierzy jakobianu F'(X). Jak widać z powyższego formatu, SNES (i kompilator...) oczekuje, że funkcja Jakobian()jest deklarowana jako int Jakobian(SNES MojSnes,Mat *Jac,Mat *Prec,int *flg,void *Ctx) i właśnie dlatego w taki, a nie inny sposób definiowaliśmy naszą procedurę Jakobian() w pliku jac2x2.c powyżej. Ostatni argument dla SNESSetJacobian() to wskaźnik do kontekstu, wykorzystywanego przez procedurę Jakobian() i zawierającego dane używane przy wyznaczaniu macierzy F'(X).

Ponieważ nasze procedury: Funkcja()oraz Jakobian() nie korzystają z kontekstu użytkownika, jako ostatni argument wywołania SNESSetFunction() i SNESSetJacobian() podajemy PETSC_NULL:

 /* Przekaz SNESowi funkcje i wektor residualny */
SNESSetFunction(MojSnes, R, Funkcja, PETSC_NULL); 

 /* Przekaz SNESowi macierz jakobianu i funkcje obliczajaca jakobian */
SNESSetJacobian(MojSnes,MatJ,MatJ,Jakobian,PETSC_NULL);

 /* Uwzglednij opcje uruchomienia SNESu typu -snes_view -snes_monitor  */
SNESSetFromOptions(MojSnes); 

Wszystkie dane o równaniu są już przekazane do SNESu, opcje ustawione, moglibyśmy więc już rozwiązać równanie... jeśli tylko określilibyśmy przybliżenie początkowe. Przybliżenie początkowe (analogicznie jak w SLESie) wpiszemy wprost do wektora rozwiązania. Właśnie do tego przydadzą się nam tablice X0 i idx, zadeklarowane na początku programu.

/* Przyblizenie poczatkowe */
OptionsGetScalar( PETSC_NULL, "-x0", &X0[0], &flg ); 
if( !flg ) X0[0] = 1.0;
OptionsGetScalar( PETSC_NULL, "-y0", &X0[1], &flg );
if( !flg ) X0[1] = 2.0;
VecSetValues(X, 2, idx, X0, INSERT_VALUES );
ierr = VecAssemblyBegin(X); CHKERRA(ierr);
ierr = VecAssemblyEnd(X); CHKERRA(ierr);

18:/home/staff/przykry/Petsc> test -y0 5.0

Po określeniu przybliżenia początkowego nie pozostaje nam już nic innego, jak nakazać SNESowi rozwiązanie naszego zadania:

SNESSolve(MojSnes,X,&its);

PetscPrintf(MPI_COMM_WORLD, "Liczba iteracji = %d\n", its);
PetscPrintf(MPI_COMM_WORLD,"Wektor rozwiazania:\n");
VecView(X, VIEWER_STDOUT_WORLD);

 VecDestroy(X); 
 VecDestroy(R);
 MatDestroy(MatJ); 
 SNESDestroy(MojSnes);
 PetscFinalize();

Makefile

include $(PETSC_DIR)/bmake/$(PETSC_ARCH)/base
CC = gcc -DPETSC_LOG
CLINKER = gcc
CFLAGS = $(PCONF) $(PETSC_INCLUDE) $(BS_INCLUDE)
LIBBASE = libpetscsles libpetscsnes
OPTS = -O
BOPT = O

OBJECTS_EX1 = uklad2x2.o fun2x2.o jac2x2.o

EXECUTABLE = test

ex1: $(OBJECTS_EX1) 
-$(CLINKER) -o $(EXECUTABLE) $(OBJECTS_EX1) \
-lm $(PETSC_LIB)

#
# ex1 source files 
#

uklad2x2.o: uklad2x2.c
$(CC) $(CFLAGS) $(OPTS) -c uklad2x2.c

fun2x2.o: fun2x2.c
$(CC) $(CFLAGS) $(OPTS) -c fun2x2.c

jac2x2.o: jac2x2.c
$(CC) $(CFLAGS) $(OPTS) -c jac2x2.c

Ćwiczenia

1. Zaimplementuj metodę iteracji prostej dla rozwiązywania równań nieliniowych, działającą analogicznie jak SNES. Testuj ją na powyższym przykładzie.
2. Naucz się obsługiwać kilka opcji uruchomienia SNESu (patrz rozdział "Co jeszcze warto wiedzieć o SNESie?" na stronie 65). Zbadaj, który wariant metody Newtona jest najbardziej efektywny na omawianym przykładzie.
3. Zmień funkcję na bardziej skomplikowaną i zobacz, jak przybliżenie początkowe wpływa na przebieg procesu zbieżności.

Nieliniowe zagadnienie różniczkowe w PETSc

Dla prostoty, to równanie będziemy aproksymować metodą różnic skończonych, dostając problem dyskretny postaci:

Problem

dla ,

.

Jak widzimy, mamy tym razem do czynienia z układem N równań nieliniowych, gdzie N oznacza liczbę wewnętrznych węzłów siatki (warunki brzegowe Dirichleta wyznaczają od razu u₀ i u_N+1, więc możemy ograniczyć się jedynie do obliczenia u w pozostałych węzłach). Jeśli więc siatka jest gęsta, to rozmiar zadania nieliniowego jest bardzo duży, a macierz pochodnej rozrzedzona. Właśnie to powoduje, że stosowanie PETSc do problemów pochodzących z dyskretyzacji nieliniowych równań różniczkowych cząstkowych zaczyna być sensowne. Narzędzia dostępne w PETSc (a więc także w SNESie) były tworzone właśnie z myślą o efektywnych metodach rozwiązywania problemów powstałych z dyskretyzacji równań różniczkowych cząstkowych.

Wstępna analiza problemu: wybór strategii

Zacznijmy od przeanalizowania problemu. To jest bardzo ważne, albowiem od tego, w jaki sposób podejdziemy do zagadnienia, będzie zależało wiele naszych następnych posunięć. Mamy do czynienia z nieliniowym zagadnieniem dyskretnym, które zamierzamy rozwiązywać metodą Newtona. Musimy więc najpierw przeformułować to zagadnienie jako zero pewnego odwzorowania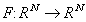. Oznaczając przez u_h wektor rozwiązania:

,

możemy zapisać zagadnienie dyskretne w postaci wektorowej: 

,

gdzie A_h oznacza macierz (minus) laplasjanu, a B_h macierz dyskretyzacji pierwszej pochodnej różnicą centralną, tzn.:

Zwróćmy uwagę, że tym razem operację mnożenia wektorów  rozumiemy nie w sensie iloczynu skalarnego, tylko jako operację mnożenia odpowiadających współrzędnych.

Przy takim zapisie łatwo już określić funkcję, której zerem będzie rozwiązanie naszego zagadnienia:

Jej pochodną będzie naturalnie taki operator liniowy , który w działaniu na wektor w da wektor F'(u)w, określony przez 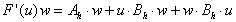. Określiliśmy więc oraz wyprowadziliśmy wzór na F'. Jak pamiętamy, SNES będzie potrzebował procedur obliczających i. Musimy teraz zastanowić się, jak zaimplementować te funkcje w PETSc. Tutaj pojawia się następna zaleta zapisu wektorowego: daje się on bardzo łatwo "przetłumaczyć" na kod źródłowy PETSc! 

Definicja funkcji F

		macierz laplasjanu pomnożona przez X funkcją MatMult()
		wynik mnożenia macierzy pierwszej pochodnej przez X, razy (po współrzędnych) X - funkcje MatMult() oraz VecPointwiseMult(),
		prawa strona

Czy z pochodną F'(u) pójdzie nam równie łatwo?... 

Pochodna F

Jak wiadomo, pochodną odwzorowania  możemy reprezentować jako macierz 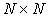. Zwróćmy jednak uwagę na pewien detal: było nam wygodniej zapisać pochodną F nie jako macierz pochodnych cząstkowych, lecz jako operator, którego wartości na zadanym wektorze w są zdefiniowane pewnym wzorem. W taki właśnie sposób definiuje się w PETSc macierze powłokowe (shell matrices), o których była mowa na stronie 18. Idea macierzy powłokowych wyjątkowo dobrze sprawdzi się w naszym zagadnieniu:

• Pochodną było nam po prostu łatwiej określić operatorowo, niż macierzowo. Niby mała rzecz, bo i tak umiemy różniczkować, ale każdy, kto doświadczył drobnej pomyłki w trakcie obliczeń na papierze, doceni fakt, że nie musimy tego robić, o ile używamy macierzy powłokowej.
• Przypomnijmy sobie, że w każdym kroku metody Newtona, macierz jakobianu F'(X) zmienia się, ponieważ zmienia się punkt, w którym jest wyznaczana. Gdybyśmy używali postaci macierzowej, za każdym razem musielibyśmy uaktualniać elementy tej macierzy. Mając macierz powłokową, nie musimy robić nic, ponieważ zmiany są uwzględniane na bieżąco.
• Do rozwiązywania układów z macierzą pochodnej F'(X) w PETSc będziemy zapewne stosować jakąś metodę iteracyjną, a te wymagają jedynie operacji mnożenia przez macierz. Ponieważ i tak na początku procesu Newtona nie mamy dobrego przybliżenia, będziemy mogli pozwolić sobie na mniej dokładne rozwiązywanie układów z macierzą jakobianu w pierwszych kilku krokach, co dramatycznie obniży koszt całego procesu. Mówimy o tym więcej w rozdziale "Inne opcje" na stronie 66.
• Wreszcie, co też jest ważne, wykorzystamy już istniejące obiekty. W definicji funkcji F używaliśmy macierzy laplasjanu i pochodnej, i teraz te same macierze posłużą nam do zdefiniowania F'. Nie będziemy w bólach definiować element po elemencie macierzy jakobianu!

Koncept kontekstu

Ktoś bardzo początkujący mógłby pomyśleć o takiej realizacji:

int Funkcja( SNES MojSnes, Vec X, Vec F, void * Ctx )
{
  Mat A, B;
  /* generuj A i B, a nastepnie przypisz im wartosci */
  MatCreate(A); MatCreate(B);
  MatSetValues(A); ...itd....

  /* uzyj A i B do obliczenia F */
  MatMult(A); VecAXPY(); MatMult(B); itd...

  /* zwolnij macierze A i B */
  MatDestroy(A); MatDestroy(B);
}

Podstawową wadą zaproponowanej procedury jest wielokrotne robienie tego samego: generowanie wciąż tych samych macierzy. Najprostszym sposobem usunięcia tego problemu byłoby jednokrotne utworzenie i wygenerowanie elementów macierzy A i B (raz, a dobrze!) gdzieś na zewnątrz procedury Funkcja(). Świetnie, ale jak skorzystać z tych macierzy wewnątrz procedury? Znów, najszybciej przychodzi nam do głowy rozwiązanie najprostsze, ale jednocześnie najbardziej bałaganiarskie: po prostu, trzeba zadeklarować te macierze jako zmienne globalne!

Mat A, B; /* nasze macierze jako zmienne globalne: 
             deklarowane na zewnatrz wszystkich funkcji */
/******************************************************
                  Program glowny
******************************************************/

int main(int argc, char **argv)
{

  /* generuj A i B, a nastepnie przypisz im wartosci */
  MatCreate(A); MatCreate(B);
  MatSetValues(A); ...itd...

  /* ......... */
  SNESSetFunction( Funkcja );

  /* ......... */
  /* zwolnij macierze A i B */
  MatDestroy(A); MatDestroy(B);
  return(0);
}

/******************************************************
              Procedura obliczajaca F(X)
******************************************************/

int Funkcja( SNES MojSnes, Vec X, Vec F, void * Ctx )
{
  /* uzyj A i B do obliczenia F */

  MatMult(A); VecAXPY(); MatMult(B); itd...
  return(0);
}

Jak taki kontekst powinien wyglądać? Zasadniczo, będzie to struktura w C, zawierająca parametry, które zechcemy przekazać do Funkcji(). Tymi parametrami mogą być macierze, wektory robocze (o tak, przydadzą się!), a nawet wskaźniki do funkcji udostępniających zmienne lokalne funkcjom używającym naszego kontekstu. Taka struktura, ze zmiennymi lokalnymi, funkcjami dostępu itp. mocno pachnie porządną klasą w C++ i tak jest w rzeczywistości: programowanie z użyciem kontekstów ma wiele cech programowania obiektowego.

Wracając do naszej konkretnej sytuacji, kontekst, jaki chcielibyśmy przekazać do Funkcji(), powinien zawierać dwie macierze: dyskretyzacji laplasjanu i pierwszej pochodnej. Kontekst ma być strukturą, więc wygodnie nam będzie najpierw zdefiniować odpowiedni typ strukturalny:

typedef struct {
  Mat A;
  Mat B;
} USERCTX;

int main(int argc, char **argv)
{
  USERCTX UserCtx;
  /* inicjalizacja kontekstu */
  USERCTXCreate( &UserCtx );
 
  /* ....wykorzystanie kontekstu.... */
  SNESSetFunction( MojSnes, X, R, Funkcja, (void *) &UserCtx );

  /* zwolnienie kontekstu */
  USERCTXDestroy( &UserCtx );
}

int USERCTXCreate( USERCTX *UserCtx )
{
  MatCreate( &UserCtx->A ); MatCreate( &UserCtx->B );
  MatSetValues( UserCtx->A ); 
  ...itd....
}
int USERCTXDestroy( USERCTX *UserCtx )
{
  MatDestroy( UserCtx->A ); ...itd...

}

int Funkcja( SNES MojSnes, Vec X, Vec F, void * Ctx )
{
  USERCTX *UserCtx;
  /* najpierw rzutujemy wskaznik na odpowiedni typ */
  UserCtx = (USERCTX *) Ctx;
  /* uzyj A i B do obliczenia F */
  MatMult( UserCtx->A, X, F ); VecAXPY(); MatMult(); itd...
  return(0);
}

Implementacja

Zaczynamy od kontekstu użytkownika

user.h

static Scalar zero = 0.0;
static Scalar one  = 1.0;

static Scalar mone = -1.0;
typedef struct
{ 
        Mat Lap;   /* macierz laplasjanu          */
        Mat Poch;  /* macierz pierwszej pochodnej */
        Vec X;     /* wektor rozwiazania          */
        Vec F;     /*        prawej strony        */
        Vec R;     /*        residuum             */
        Vec y;     /*        pomocniczy           */
        Vec z;     /*        pomocniczy           */

} USERCTX;

Dodatkowo, zdefiniowaliśmy parę stałych typu Scalar, bardzo przydatnych do wykonania operacji obliczenia sumy lub różnicy dwóch wektorów przy pomocy funkcji VecAXPY(). Będą one dostępne w każdym pliku zawierającym dyrektywę #include "user.h".

Implementacja funkcjiF(X)

cdfun.c

#include "snes.h" /* plik z definicjami funkcji i obiektow SNES; zawiera takze
                     dyrektywe #include "sles.h" */

#include "user.h" /* kontekst uzytkownika i przydatne stale */

/******************************************************
        Procedura obliczajaca wartosci funkcji F
******************************************************/

int Funkcja(SNES MojSnes,Vec X,Vec F,void *Ctx)
{
int    ierr;
USERCTX *UserCtx = (USERCTX *)Ctx;

  /* Pomnoz przez pochodna centralna... */

  ierr = MatMult( UserCtx->Poch, X, UserCtx->y ); CHKERRQ(ierr);

  /* ...i domnoz przez u */
  ierr = VecPointwiseMult( X, UserCtx->y, F ); CHKERRQ(ierr);

  /* Pomnoz przez laplasjan */
  ierr = MatMult( UserCtx->Lap, X, UserCtx->y ); CHKERRQ(ierr);

  /* Zsumuj! */
  ierr = VecAXPY( &one, UserCtx->y, F ); CHKERRQ(ierr);
  ierr = VecAXPY( &mone, UserCtx->F, F ); CHKERRQ(ierr);
  return(ierr);
}

Implementacja macierzy pochodnej F'(X)

cdjac.c

/******************************************************
                 Definicja pochodnej F
******************************************************/
#include "snes.h"
#include "user.h"

/* Implementacja funkcji Jakobian(), przekazywanej do SNESu */

int Jakobian(SNES MojSnes, Vec X, Mat *Jac, 
                Mat *Precond, MatStructure *flag, void *Ctx)
{
  *flag = SAME_NONZERO_PATTERN;
  return(0);
}

/* Implementacja mnozenia przez macierz jakobianu */

int MultJakobian( Mat Jac, Vec VecIn, Vec VecOut )
{
int ierr;
USERCTX *UserCtx;

  /* Najpierw musimy wydobyc kontekst */
  ierr = MatShellGetContext( Jac, (void **)&UserCtx );CHKERRQ(ierr);

  /* Pomnoz przez pochodna centralna... */
  ierr = MatMult( UserCtx->Poch, VecIn, UserCtx->y ); CHKERRQ(ierr);

  /* ...i domnoz przez u */
  ierr = VecPointwiseMult( UserCtx->X, UserCtx->y, VecOut ); CHKERRQ(ierr);
  /* Pomnoz przez laplasjan */
  ierr = MatMult( UserCtx->Lap, VecIn, UserCtx->y ); CHKERRQ(ierr);
  /* Zsumuj! */
  ierr = VecAXPY( &one, UserCtx->y, VecOut ); CHKERRQ(ierr);
  ierr = MatMult( UserCtx->Poch, UserCtx->X, UserCtx->y ); CHKERRQ(ierr);
  ierr = VecPointwiseMult( VecIn, UserCtx->y, UserCtx->z ); CHKERRQ(ierr);

  ierr = VecAXPY( &one, UserCtx->z, VecOut ); CHKERRQ(ierr);

  return(ierr);
}

Ponieważ wszystko załatwia operacja mnożenia, jest to dobre miejsce na zdefiniowanie procedury mnożenia wektora przez macierz jakobianu. Ta procedura zostanie potem przekazana jako argument MatShellSetOperation(), dopełniając definiowanie powłokowej macierzy F'(X). Procedurę MultJakobian(), definiującą de facto macierz F'(X), wykorzystamy przy okazji tworzenia powłokowej macierzy jakobianu w programie głównym.

Program główny: wykorzystanie SNESu

cd.c

#include <stdio.h>
#include <math.h>   /* zawiera funkcje sin(x) */
#include "snes.h"
#include "user.h"

static char help[] = "Rozwiazuje nieliniowe jednowymiarowe rownanie\n\ 
konwekcji-dyfuzji na odcinku [0,L]\n\
Opcje: -N [int] liczba wewnetrznych wezlow siatki\n\
       -L [Scalar]  dlugosc odcinka\n\n";

/* Deklaracje procedur obliczajacych funkcje i jakobian */
extern int MultJakobian( Mat, Vec, Vec);
int Jakobian(SNES,Vec,Mat*,Mat*,MatStructure*,void*);
int Funkcja(SNES,Vec,Vec,void*);
int USERCTXCreate(USERCTX*,int,Scalar);
int USERCTXDestroy(USERCTX*);

/**************************************************************
                     Program glowny 
**************************************************************/

int main( int argc, char **argv )
{
  SNES     MojSnes;        /* obiekt SNES, ktorym rozwiazemy zadanie */
  Mat      MatJ;           /* macierz jakobianu */
  USERCTX  UserCtx;        /* kontekst uzytkownika */
  int      n;              /* liczba wezlow siatki */
  static Scalar L = M_PI;  /* dlugosc przedzialu calkowania, 
                              zatem krok siatki h = L/n */
  int      ierr, flg, its;
 
  PetscInitialize( &argc, &argv,PETSC_NULL,help );

  /* Interpretacja opcji uzytkownika */
  ierr = OptionsGetInt( PETSC_NULL, "-N", &n, &flg ); CHKERRA(ierr);
  if( !flg ) n = 3;
  ierr = OptionsGetScalar( PETSC_NULL, "-L", &L, &flg );
  CHKERRA(ierr); 

  /* Tworzenie potrzebnych obiektow: SNESu, wektorow, macierzy pomocniczych */
  ierr = SNESCreate(MPI_COMM_WORLD,SNES_NONLINEAR_EQUATIONS,&MojSnes); CHKERRA(ierr);
  ierr = USERCTXCreate( &UserCtx, n, L ); CHKERRA(ierr);
  VecView( UserCtx.F, VIEWER_DRAWX_WORLD  ); PetscSleep(5);

  /* Przekaz SNESowi funkcje i wektor residualny */
  ierr = SNESSetFunction(MojSnes, UserCtx.R, Funkcja, &UserCtx); CHKERRA(ierr);

  /* Przekaz SNESowi macierz jakobianu i funkcje obliczajaca jakobian */
  ierr = MatCreateShell(MPI_COMM_WORLD,n,n,n,n,&UserCtx,&MatJ); CHKERRA(ierr);
  ierr = MatShellSetOperation(MatJ, MATOP_MULT, MultJakobian ); CHKERRA(ierr);
  ierr = SNESSetJacobian(MojSnes,MatJ,MatJ,Jakobian,&UserCtx); CHKERRA(ierr);

  /* Uwzglednij opcje uruchomienia SNESu typu -snes_view -snes_monitor  */
  ierr = SNESSetFromOptions(MojSnes); CHKERRA(ierr);

  /* Rozwiaz! */
  ierr = SNESSolve(MojSnes,UserCtx.X,&its); CHKERRA(ierr);
  
  PetscPrintf(MPI_COMM_WORLD, "Liczba iteracji = %d\n", its);
  PetscPrintf(MPI_COMM_WORLD,"Wektor rozwiazania:\n");
  ierr = VecView(UserCtx.X, VIEWER_DRAWX_WORLD); CHKERRA(ierr);
  PetscSleep( 10 );

  /* Zwolnij pamiec */
  ierr = USERCTXDestroy(&UserCtx); CHKERRA(ierr); 
  ierr = MatDestroy(MatJ); CHKERRA(ierr); 
  ierr = SNESDestroy(MojSnes); CHKERRA(ierr);
  PetscFinalize();
  return 0;
}

/**************************************************************
            Funkcje zwiazane z kontekstem uzytkownika
**************************************************************/

int USERCTXCreate( USERCTX * UserCtx, int n, Scalar L )
{
extern int GenerujLaplasjan1D( Mat, Scalar );
extern int GenerujPochodnaCentralna1D( Mat, Scalar ); 
int ierr=0;
int i;
double val;
double h = L/(n+1); /* krok siatki */
   
  /* tworzymy wektory uzywane w kontekscie naszego zagadnienia */
  ierr = VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,n,&UserCtx->X); CHKERRQ(ierr);
  ierr = VecDuplicate(UserCtx->X,&UserCtx->R); CHKERRQ(ierr);
  ierr = VecDuplicate(UserCtx->X,&UserCtx->F); CHKERRQ(ierr);
  ierr = VecDuplicate(UserCtx->X,&UserCtx->y); CHKERRQ(ierr);
  ierr = VecDuplicate(UserCtx->X,&UserCtx->z); CHKERRQ(ierr);

  /* tworzymy macierze uzywane w kontekscie naszego zagadnienia */
  ierr = MatCreate(MPI_COMM_WORLD,n,n,&UserCtx->Lap); CHKERRQ(ierr);
  ierr = MatCreate(MPI_COMM_WORLD,n,n,&UserCtx->Poch); CHKERRQ(ierr);

  /* generujemy elementy macierzy pomocniczych */
  ierr = GenerujLaplasjan1D( UserCtx->Lap, (Scalar) h ); CHKERRQ(ierr);
  ierr = MatView( UserCtx->Lap, VIEWER_DRAWX_WORLD ); CHKERRQ(ierr);
  PetscSleep( 3 );

  ierr = GenerujPochodnaCentralna1D( UserCtx->Poch, (Scalar) h );CHKERRQ(ierr);

  ierr = MatView( UserCtx->Poch, VIEWER_DRAWX_WORLD ); CHKERRQ(ierr);

  PetscSleep( 3 );

  /* generujemy prawa strone */
  for( i = 1 ; i <= n ; i++ )
  {
        val = sin(i*h) + sin(i*h)*cos(i*h); /* rozwiazanie u(x) = sin(x) */
        VecSetValue( UserCtx->F, i-1, (Scalar)val, INSERT_VALUES );
  }
  /* Przyblizenie poczatkowe */
  /* Zakladamy, ze zerowe... Od razu wpisujemy do wektora rozwiazania X */

  ierr = VecSet(&zero, UserCtx->X); CHKERRQ(ierr);
  return(ierr);
}

int USERCTXDestroy( USERCTX * UserCtx )
{
int ierr;
  ierr = VecDestroy(UserCtx->X); CHKERRQ(ierr); 
  ierr = VecDestroy(UserCtx->R); CHKERRQ(ierr);
  ierr = VecDestroy(UserCtx->F); CHKERRQ(ierr);
  ierr = VecDestroy(UserCtx->z); CHKERRQ(ierr);
  ierr = VecDestroy(UserCtx->y); CHKERRQ(ierr);
  ierr = MatDestroy(UserCtx->Lap); CHKERRQ(ierr);
  ierr = MatDestroy(UserCtx->Poch); CHKERRQ(ierr);
  return(ierr);
}

Po wstępnych #include następuje lista prototypów procedur - zdefiniowanych gdzie indziej, np. w innych plikach - a wykorzystywanych poniżej. Przydaje się to kompilatorowi dla pełniejszego sprawdzania poprawności wywołań tych funkcji. W samej funkcji main() deklarujemy na początku kilka zmiennych lokalnych, w tym obiekt SNESu MojSnes, macierz (za chwilę okaże się, że powłokową) jakobianu MatJ oraz kontekst UserCtx, zawierający m.in. macierze laplasjanu i pierwszej pochodnej, a także wektory rozwiązania i residuum. Zaczynamy klasycznie, od inicjalizacji PETSc oraz ściągnięcia opcji użytkownika:

PetscInitialize( &argc, &argv,PETSC_NULL,help );
/* Interpretacja opcji uzytkownika */
OptionsGetInt( PETSC_NULL, "-N", &n, &flg );
if( !flg ) n = 3;
OptionsGetScalar( PETSC_NULL, "-L", &L, &flg );

/* Tworzenie potrzebnych obiektow: SNESu, wektorow, macierzy pomocniczych */
SNESCreate(MPI_COMM_WORLD,SNES_NONLINEAR_EQUATIONS,&MojSnes); 
USERCTXCreate( &UserCtx, n, L );

/* Przekaz SNESowi funkcje i wektor residualny */
SNESSetFunction(MojSnes, UserCtx.R, Funkcja, &UserCtx);

MatCreateShell(MPI_COMM_SELF,n,n,n,n,&UserCtx,&MatJ);
MatShellSetOperation(MatJ, MATOP_MULT, MultJakobian );

SNESSetJacobian(MojSnes,MatJ,MatJ,Jakobian,&UserCtx);

Funkcje związane z kontekstem USERCTX

Ćwiczenia

1. Uzupełnij powyższy program o funkcję GenerujLaplasjan1D() i przetestuj dla rozmaitych prawych stron zagadnienia konwekcji-dyfuzji.
2. Rozwiąż zagadnienie konwekcji-dyfuzji w obszarze dwuwymiarowym.
3. Rozwiąż zagadnienie , z jednorodnymi warunkami brzegowymi Dirichleta.
4. Zastanów się, jak wykorzystać moc SNESu do implementacji metody typu Predyktor-Korektor rozwiązywania układu równań różniczkowych zwyczajnych. (Na każdym kroku schematu PC będziemy musieli rozwiązać równanie nieliniowe!)
5. Trudne, ale warto... Napisz program, rozwiązujący równanie Naviera-Stokesa w obszarze L-kształtnym:


Wybór schematu numerycznego dla aproksymacji tego równania nie jest trywialny.

Co jeszcze warto wiedzieć o SNESie?

Warianty metody Newtona

Metody poszukiwania kierunkowego

Możemy teraz wybierać stopień wielomianu interpolacyjnego używanego do wyznaczenia lepszego czynnika skalującego: -snes_eq_ls [quadratic,cubic], to znaczy, odpowiednio, funkcją kwadratową lub sześcienną. Więcej szczegółów Czytelnik znajdzie u Kelley'a [11] oraz w [14]. Dodatkowo, możliwy jest także wariant
-snes_eq_ls basic. Taki wybór oznacza rezygnację z techniki line search i pozostanie przy klasycznej metodzie Newtona.

Metody wyszukiwania kierunkowego wymagają ustawienia pewnych parametrów relaksacyjnych,
-snes_eq_ls_alpha <alpha>, -snes_eq_ls_maxstep <max>, -snes_eq_ls_steptol <tol>, gdzie oznaczenia są zgodne z [4]. Na szczęście, predefiniowane wartości tych parametrów są zazwyczaj rozsądne dla wielu zagadnień. 

Parametry stopu

• atol,
• rtol,
• stol.

ierr = SNESSetTolerances(SNES snes,double rtol,double atol,double stol, int maxits,int maxfcts);

lub z linii komend: -snes_atol <atol>, -snes_rtol <rtol>, -snes_stol <stol>,
-snes_max_it <maxits> oraz -snes_max_funcs <maxfcts>. 

Inne opcje

Zmianę opcji SLESu wykorzystywanego przez SNES możemy uzyskać z programu, wyłuskując kontekst SLESu funkcją int SNESGetSLES( SNES MojSnes, SLES * MojSnesSles ) a następnie używając procedur typu SLESGetKSP() lub SLESGetPC(). Naturalnie, to samo uzyskamy podając odpowiednie opcje w linii komend.

Zazwyczaj programy (w początkowym stadium) nie są wolne od błędów. Można się w szczególności obawiać, że zaprogramowana przez nas macierz jakobianu nie jest idealna. Na szczęście, możemy porównać działanie programu z naszą macierzą jakobianu i programu, w którym zostanie użyta jej aproksymacja metodą różnic skończonych. W wypadku, gdy używamy macierzy typu powłokowego, możemy naszą funkcję Jakobian(), realizującą działanie jakobianu, zastąpić jej aproksymacją generowaną wewnętrznie przez PETSc metodą różnic skończonych: wystarczy uruchomić program z opcją -snes_mf. Podobny skutek można uzyskać (ale już tylko dla niepowłokowej macierzy jakobianu) stosując opcję -snes_fd. Nie znamy bliżej różnic między tymi opcjami. Po co stosować te opcje? Na pewno przydadzą się one tym, którzy nie potrafią (lub nie mają czasu) implementować funkcji Jakobian(). Czasem macierz jakobianu może być skomplikowana! Autorzy oficjalnego manuala twierdzą ponadto, że możemy w ten sposób łatwo sprawdzić, czy poprawnie zaimplementowaliśmy jakobian: bo jeśli nie, to, rozwiązując zagadnienie raz z własnym jakobianem, a drugi raz z opcją -snes_mf, powinniśmy dostać istotnie różniące się wyniki. To prawda, ale od razu chcielibyśmy ostrzec wszystkich pesymistów: jeśli postępując w wyżej opisany sposób, rzeczywiście dostaniecie różne wyniki (rozwiązania, liczbę iteracji, itp.) nie wpadajcie w desperację. Jest bardzo prawdopodobne, że po prostu rozwiązujecie swoje zadanie z niedobrymi parametrami! Pamiętajcie, że wyznaczenie aproksymacji jakobianu jest numerycznie bardzo kosztowne (wymaga za każdym razem obliczania wielu wartości Funkcji()) a jednym z ograniczeń ustawianym w SNESie jest właśnie liczba wywołań funkcji!

Śledzenie pracy SNESu

Ponadto, każdy SNES posiada (oczywiście!...) swoją przeglądarkę, wyświetlającą parametry wywołania SNESu: int SNESView(SNES snes,Viewer viewer), gdzie, jak zwykle, jako viewer możemy podać VIEWER_STDOUT_WORLD. Z linii komend uzyskamy ten sam efekt podając opcję -snes_view. Oto przykładowy wynik obejrzenia SNESu:

SNES Object:
  method: ls

    line search variant: SNESCubicLineSearch
    alpha=0.0001, maxstep=1e+08, steptol=1e12
  maximum iterations=50, maximum function evaluations=1000
  tolerances: relative=1e-08, absolute=1e-50, truncation=1e-12, solution=1e-08
  total number of linear solver iterations=13
  total number of function evaluations=6
KSP Object:
  method: gmres
    GMRES: restart=30, using Modified GramSchmidt Orthogonalization
  maximum iterations=10000, initial guess is zero
  tolerances:  relative=1e-05, absolute=1e-50, divergence=10000
  left preconditioning
PC Object:
  method: none
  linear system matrix = precond matrix:
Matrix Object:

  type=MATSHELL, rows=343, cols=343

Podsumowanie SNESu

• obiekt typu SNES: MojSnes - służący do rozwiązywania równań nieliniowych;
• wektory: R - wektor residuum, X - wektor rozwiązania (przed uruchomieniem SNESSolve() wpisujemy do niego przybliżenie początkowe!);
• macierze: Jac - macierz jakobianu, Prec - macierz, na podstawie której będzie budowany preconditioner dla Jac (zazwyczaj wystarcza wziąć Jac jako Prec);
• funkcje:

int Jakobian(SNES MojSnes,Vec X,Mat *Jac,Mat *Prec,int *flag, void *JacCtx); funkcja wyznaczająca macierz jakobianu Jac i preconditionera Prec na podstawie wartości rozwiązania na kolejnym kroku X; w wyniku musi ustawiać wartość paramteru flag identyfikującego zmianę struktury macierzy Prec, analogicznie jak w SLESSetOperators(); opis użycia tej funkcji w przypadku, gdy te macierze są macierzami powłokowymi znajduje się w rozdziale "Definicja funkcji F" na stronie 57.

• konteksty użytkownika: FunCtx - struktura w C, czyli kontekst, zawierający parametry i prywatne zmienne potrzebne do wyliczenia F(X), wykorzystywany przez Funkcja(); JacCtx - kontekst zawierający parametry i prywatne zmienne potrzebne do wyliczenia F'(X), wykorzystywany przez Jakobian(); najczęściej, tworzymy jeden wspólny dla obu funkcji kontekst; jeśli nie korzystamy z kontekstów, przekazujemy do odpowiednich funkcji PETSC_NULL.

• komunikator MPI: comm, u nas zawsze podajemy MPI_COMM_WORLD;
• tryb uruchomienia SNESu: mode - u nas zawsze będzie to SNES_NONLINEAR_EQUATIONS - sygnalizujemy, że SNES będzie wykorzystany do rozwiązania układu równań nieliniowych; inna możliwa wartość tego parametru to SNES_UNCONSTRAINED_MINIMIZATION, dzięki której wygenerujemy SNES w kontekście rozwiązywania zagadnień optymalizacyjnych (niestety, zmienia się wtedy także cały schemat użycia SNESu);
• przeglądarka dla SNESu: viewer - musi być tekstowa, u nas zawsze VIEWER_STDOUT_WORLD;
• its - liczba iteracji wykonanych przez SNES; w przypadku stwierdzenia niezbieżności, liczba podawana jest ze znakiem minus.

Zarówno procedura obliczająca funkcję F(X), jak procedura obliczająca jakobian F'(X), muszą być ściśle określonego typu. Przed użyciem SNESu, musimy wygenerować niezłe przybliżenie początkowe. Efektywność całego procesu rozwiązywania równania będzie zależała przede wszystkim od sposobu implementacji F(X) oraz F'(X). Warto także zastanowić się, czy dobrze są dobrane parametry SNESu.

O czym nie napisaliśmy

Oprócz SLESu i SNESu, mamy także moduł TS (ang. time stepping), z implementacją metod różnicowych rozwiązywania wielkich układów równań różniczkowych zwyczajnych powstałych na przykład po dyskretyzacji (względem zmiennej przestrzennej) równania parabolicznego. Dodajmy, że PETSc ma możliwość wykorzystywania w tym celu także biblioteki zewnętrznej PVODE autorstwa A.Hindmarsha i in., będącej równoległą wersją biblioteki CVODE (dość wyrafinowanych metod wielokrokowych).

PETSc posiada wiele opcji profilowania kodu. Jedną z nich można uruchomić dodając do linii komend
-petsc_log. Użytkownik ma wtedy możliwość sprawdzenia, ile czasu CPU (lub jaki procent obliczeń) pochłania wybrany fragment kodu. Można też śledzić sposób wykorzystywania pamięci, obciążenie poszczególnych procesorów, itp. Poza wydrukiem tekstowym, jest także możliwość obejrzenia przebiegu pracy programu w okienku graficznym. Przyznajemy, że trochę żałujemy, iż do tej pory nie zaczęliśmy w pełni wykorzystywać tych opcji.

Dodatkowo, dla prawdziwych i porządnych programistów-profesjonalistów, PETSc daje możliwość podłączenia debuggera - zarówno dopiero po wystąpieniu błędu, jak też od początku pracy programu. Debugger może się podłączać na każdym procesorze w osobnym okienku - każdy, kto doświadczył koszmaru programowania równoległego, wie, jakie to może być ważne. I znów, jako nieprofesjonaliści, nie korzystamy z tej sposobności, gorzej, nawet nie bardzo wiemy jak obsługiwać dbx. Powód jest prozaiczny: po prostu do tego stopnia zepsuci jesteśmy pięknymi, przyjaznymi i naprawdę porządnymi debuggerami ze środowiska MS Windows (a nawet DOS!), że uczenie się topornego, tekstowego dbx'a wydaje się nam niepotrzebną męką: porównanie dbx'a i debuggera dla (powiedzmy) Visual C++ wypada tak, jak porównanie edytora vi z (powiedzmy) MS Word. Dlatego wolimy poczekać, aż pojawią się porządne debuggery także w Unix'ie (albo, o zgrozo, Windows wyprze i ten system...). Niemniej, osoby chętne, a tym bardziej pragnące pisać duże aplikacje, zachęcamy do wykorzystywania dostępnych debuggerów: jest to inwestycja, która prędzej, czy później, sowicie się opłaci!

Dalej, PETSc dysponuje pewnymi możliwościami graficznymi, ale szczerze powiedziawszy, lepiej nie używać procedur PETSc do wizualizacji: sensowniej jest wykorzystać zewnętrzne programy wizualizacji danych, na przykład AVS, Vigie, czy nawet Matlab. Warto natomiast skorzystać z grafiki PETSc dla obserwacji zachowania własnych obiektów lub procedur. Można w szczególności napisać własne - lepsze! - przeglądarki obiektów itp.

PETSc jest tworzone jako biblioteka otwarta. Jak już wspominaliśmy, PETSc może korzystać z zewnętrznej biblioteki PVODE; jest też port do kilku innych. Między innymi, do bibliotek równoległych BlockSolve95 i SPAI, z dodatkowymi solverami równań liniowych oraz do biblioteki matematycznej IBM ESSL; do Matlaba - dla wizualizacji i ewentualnego postprocessingu numerycznego; do narzędzia wizualizacji trójwymiarowych obiektów przy użyciu VRML (virtual reality), itd.

Najistotniejszą cechą PETSc, która czyni z niej naprawdę poważne narzędzie, jest przejście na programowanie równoległe na wyższym poziomie. To właśnie, w połączeniu z dostępnością podstawowych solverów i narzędzi numerycznych, stanowi prawdziwą smakowitość PETSc! Dlatego zamierzamy w ewentualnej drugiej części tego podręcznika przystępnie wyłożyć generalne zasady programowania równoległego oraz wykorzystania PETSc do (w miarę bezbolesnego) pisania efektywnych aplikacji równoległych, służących rozwiązywaniu równań różniczkowych cząstkowych. Na razie zachęcamy do własnego eksperymentowania z programami równoległymi, wykorzystującymi MPI do uruchamiania jednej aplikacji na kilku stacjach roboczych, co może pozwolić przede wszystkim na rozwiązywanie dużo większych zadań dyskretnych.

Zachęcamy do uczenia się PETSc. To naprawdę szybsze, niż kodowanie wszystkiego od zera...

Bibliografia

1. E. Anderson, Z. Bai, C. Bischof, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, S. Ostrouchov, D. Sorensen: LAPACK Users Guide - Release 2.0, SIAM, February 1995
2. Satish Balay and William D. Gropp, Lois Curfman McInnes, Barry F. Smith: PETSc 2.0 Users Manual., ANL-95/11 - Revision 2.0.22, Argonne National Laboratory, 1998. Można znaleźć w katalogu $(PETSC_DIR)/docs/ lub na stronie domowej PETSc. Znajdują się tam dwie wersje: manual.html (do oglądania przeglądarką WWW) i manual.ps (plik w Postscripcie).
3. Satish Balay and William D. Gropp and Lois Curfman McInnes and Barry F. Smith: PETSc man pages. Zawierają opis wszystkich funkcji PETSc. Można je znaleźć w katalogu $(PETSC_DIR)/docs, lub na stronie domowej PETSc.
4. Jr. Dennis, John E. and Robert B. Schnabel. Numerical methods for unconstrained optimization and nonlinear equations. Prentice­Hall Series in Computational Mathematics. Prentice­Hall Inc., Englewood Cliffs, N.J., 1983.
5. Jack J. Dongarra, Iain S. Duff, Danny C. Sorensen, and Henk A. van der Vorst. Solving linear systems on vector and shared memory computers. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1991.
6. Maksymilian Dryja, Janina i Michał Jankowscy: Przegląd metod i algorytmów numerycznych. Wydawnictwa Naukowo-Techniczne, Warszawa 1988.
7. Stanley C. Eisenstat and Homer F. Walker: Choosing the forcing terms in an inexact Newton method. SIAM J. Sci. Comput., 17(1):16--32, 1996. Special issue on iterative methods in numerical linear algebra (Breckenridge, CO, 1994).
8. G.H. Golub and Ch.F. Van Loan: Matrix computations. Johns Hopkins Studies in the Mathematical Sciences, Johns Hopkins University Press, Baltimore, MD 1996
9. W. D. Gropp: The Message Passing Interface (MPI) standard
10. W. Hackbusch: Iterative solution of large sparse systems of equations, Applied Mathematical Sciences, vol. 95, Springer-Verlag, New York 1994
11. C. T. Kelley: Iterative methods for linear and nonlinear equations, volume 16 of Frontiers in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1995. With separately available software.
12. Brian W. Kernighan, Dennis M. Ritchie: Język C, Wydawnictwa Naukowo Techniczne, Warszawa 1988.
13. Jorge J. Mor'e, Danny C. Sorensen, Burton G. Garbow, and Kenneth E. Hillstrom: The MINPACK project. In Wayne R. Cowell, editor, Sources and Development of Mathematical Software, pages 88--111. 1984.
14. Jorge J. Mor'e and David J. Thuente: Line search algorithms with guaranteed sufficient decrease. ACM Trans. Math. Software, 20(3):286--307, 1994.
15. J. M. Ortega and W. C. Rheinboldt. Iterative solutions of nonlinear equations in several variables. Academic Press, New York, 1970.
16. Barry Smith, Petter Bjřrstad, Willam Gropp: Domain Decomposition - Parallel Multilevel Methods for Elliptic Partial Differential Equations, Cambridge University Press 1996.
17. G. W. Stewart: Afternotes on numerical analysis. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1996.
18. J. Stoer and R. Bulirsch: Wstęp do analizy numerycznej. Biblioteka matematyczna. PWN, Warszawa, 1995