PROBLEM
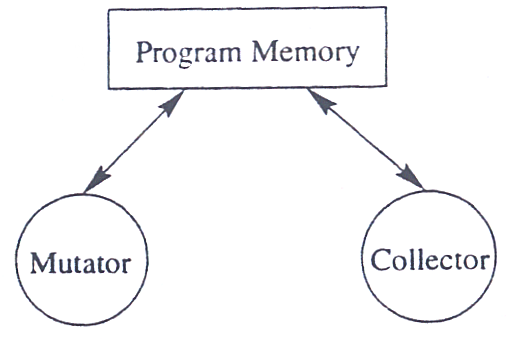
Garbage Collection, czyli odśmiecanie, polega na automatycznym zwalnianiu pamięci zaalokowanej przez program, a już przez niego nieużywanej. Odbywa się ono "w locie", co oznacza, że Garbage Collector działa równolegle z programem.
Poprawny algorytm odśmiecania powinien posiadać dwie własności:Algorytm Ben-Ari'ego jest jednym z prostszych algorytmów odśmiecania. Dzięki temu nadaje się do modelowania w CWB.
ALGORYTM
Pamięć składa się z węzłów (nodes). Każdy węzeł ma kolor - czarny lub biały - oraz ustaloną liczbę 'synów' - wskaźników na węzły. Część węzłów to korzenie - węzły zawsze dostępne dla programu. Wśród węzłów dwa są wyrożnione:
Odwołania programu do pamięci reprezentuje w modelu Mutator. Jest on maksymalnie uproszczony i wykonuje tylko jedną istotną z punktu widzenia problemu operację: przekierowuje wskaźnik dostępnego węzła na dowolny dostępny węzeł. Operacja ta nie może uczynić węzła niedostępnego dostępnym, ale może uczynić węzeł dostępny niedostępnym.
Mutator (Zmieniacz ?)
Ostatnim elementem modelu jest Collector. W jednym cyklu maluje na czarno wszystkie dostępne węzły, a następnie zbiera (odśmieca) wszystkie węzły, które pozostały białe. Są one dodawane do listy wolnych węzłów (free list).
Collector (Zbieracz ?)

MODEL W CWB
Naszym celem jest sprawdzenie, czy algorytm Ben-Ari'ego jest bezpieczny i żywotny. Aby sprawdzić bezpieczeństwo musimy wiedzieć, kiedy węzeł jest dostępny oraz kiedy jest zbierany (odśmiecany). Aby zbadać żywotność wystarczy wiedzieć, kiedy węzeł jest dostępny.
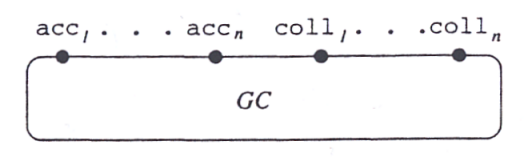
Założenie upraszczające: każdy węzeł ma jednego syna.
Zakładamy, że jest N węzłów. Są one ponumerowane liczbami do 1 do N. Pierwsze R węzłów to korzenie. Węzeł nil ma numer 1, a fl - 2.
Pamięć została wymodelowana jako jeden sparametryzowany proces. Parametrami są dwie tablice: kolorów oraz synów poszczególnych węzłów. Można próbować modelować pamięć na inne sposoby, np. każdy węzeł jako osobny proces, jednak przyjęty model jest najprostszy, a przez to najodpowiedniejszy.

Mutator

Collector

Znaczenie cl zostanie wyjaśnione później.
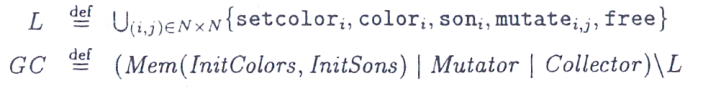
Cały system wygląda następująco:
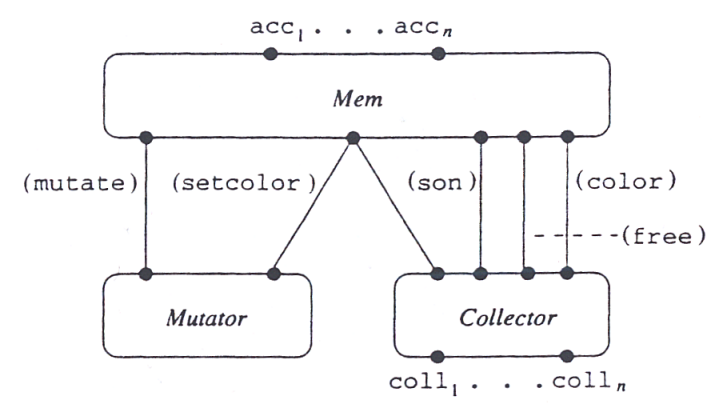
Aby udało się cokolwiek zrobić w CWB musimy niestety ograniczyć N (liczbę węzłów) do 4. Zakładamy zatem, że N = 4, R = 2. Czyli jedyne dostępne węzły to nil i fl.
WŁASNOŚCI
Możemy najpierw sprawdzić, czy w tak zdefiniowanym systemie nie ma blokad. CWB odpowiada, że nie. Co ciekawe, sprawdzenie tego zajmuje istotnie więcej czasu niż sprawdzanie pozostałych własności.Możemy teraz przejść do sprawdzania własności bezpieczeństwa i żywotności. Wyrazimy jako formuły rachunku mu.
Bezpieczeństwo
Bezpieczeństwo oznacza, że węzeł, który jest dostępny nie może zostać zebrany. Czyli, odwołując się do zdefiniowanych zdarzeń: acci i colli nie mogą zajść jednocześnie (ściślej - nie może być możliwości wykonania ich obydwu).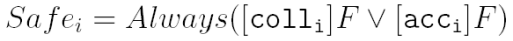
Żywotność (wersja I)
Żywotność oznacza, że każdy węzeł musi być w końcu dostępny. Czyli: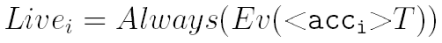
CWB odpowiada, że własność ta jest spełniona dla 1 i 2, co nie jest dziwne, ponieważ korzenie zawsze są dostępne. Okazuje się natomiast, że własność nie jest spełniona dla 3 i 4.
Przyczyną jest następująca ścieżka: najpierw stan 3 staje się niedostępny, a następnie system w nieskończoność wykonuje zdarzenie acc1 (i analogiczne do niej). Po prostu w CCS nic nie gwarantuje, że Collector będzie działał - ma się on prawo nic nie robić, jeśli jakiś inny proces chce coś robić (tu Mem zgłasza acci).
Żywotność (wersja II)
Problemem wersji I jest brak uczciwości (fairness) w CCS. Należy zatem zmienić formułe tak, by brała to pod uwagę. Tzn. chcemy napisać formułę: dla każdego węzła acci jest w końcu osiągane, o ile Collector działa. Aby wyrazić to, że Collector działa, wprowadzona zostało zdarzenie cl.
W wersji I po rozwinięciu własność żywotności wygląda tak:
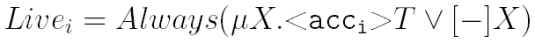
Zmienimy ją w następujący sposób:
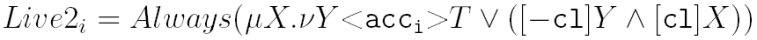
Ta własność jest spełniona dla wszystkich i. System jest żywotny.
Żywotność (wersja III)
Autor proponuje jeszcze jedno sformułowanie żywotności, tym razem odwołujące się do colli.
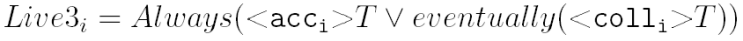
Nie precyzuje jednak, co rozumie przez eventually. Jeśli przyjąć klasyczną definicję Ev, własność nie jest spełniona z tego samego powodu co wersja I żywotności.
Ciekawsza jest druga interpretacja, gdzie eventually jest rozumiane tak, jak w wersji II. Okazuje się, że własność również nie jest spełniona. Przyczyna leży w nieatomowości zbierania. Collector najpierw wykonuje colli, a potem freei. Pokazuje to następująca ścieżka:
Węzeł 3 ma zostać zebrany. Wykonuje się coll3. W tym momencie jesteśmy w stanie, w którym nie zachodzi < acc3 >T, zatem musi zachodzić eventually(< coll3 >T). Ale jeśli węzeł 3 już nigdy nie stanie się niedostępny, to coll3 nigdy nie zajdzie - formuła nie jest spełniona.
INNE MODELE
Mutator bez zaczerniania
Wątpliwości w algorymie Ben-Ari'ego może początkowo budzić drugi krok Mutator, czyli zaczernianie węzła. Możemy użyć CWB do sprawdzenia, czy jest on rzeczywiście potrzebny.
Okazuje się, że model stracił własność bezpieczeństwa. Przyczynę ilustruje następujący rysunek:
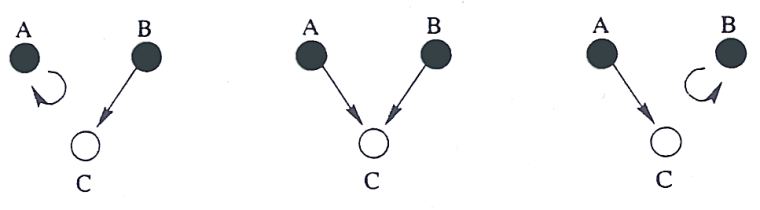
Własności bezpieczeństwa zachowują się tak samo jak w oryginalnym modelu.
Mutator odwrócony
Ben-Ari twierdził, że jego algorytm jest odporny na zamianę kolejności kroków w Mutator (tzn. najpierw zaczerniamy, a potem podmieniamy wskaźnik). Zostało jednak pokazane, że nie jest to prawda, a dokładniej, że po zamianie tracone jest bezpieczeństwo. Sprawdzimy, czy w nasz model to potwierdzi.
Kod w VP-CCS. W tym wariancie zmiany w modelu były nietrywialne.
Okazuje się niestety, że własność bezpieczeństwa została zachowana. Podobnie jest z własnościami bezpieczeństwa. Model z czterema węzłami jest najprawdopodobniej zbyt ubogi, aby bezpieczeństwo zostało utracone.
Bezpieczeństwo poprzez blokady
Możemy spróbować alternatywnego podejścia do sprawdzania bezpieczeństwa algorytmu. Mianowicie możemy tak zmienić proces Mem, by próba zebrania dostępnego węzła wywoływała blokadę. Dzięki temu możemy zapomnieć o zdarzeniach acci i colli. CWB potwierdza przypuszczenie, że system nie ma blokad. Zatem jest bezpieczny.PODSUMOWANIE
Udało się stworzyć rozsądny model dla algorytmu Ben-Ari'ego dość zwięzły, by dało się go wprowadzić do CWB, a nawet pokazać istotne własności: bezpieczeństwo i żytwotność. Trzeba sobie jednak zdać sprawę z wielu ograniczeń.
Na potrzeby modelu musieliśmy ukonkretyzować pewne idee, które mogą w konkretnych implementacjach algorytmu Ben-Ari'ego być zrealizowane inaczej. Dla przykładu: algorytm nie precyzuje w jaki sposób zbierane węzły mają zostać wstawiane na listę wolnych węzłów - my wstawiamy węzły zawsze na początek listy. Trudno przewidzieć, jaki ma to wpływ na prawdziwość interesujących nas własności.
Z przyczyn praktycznych N jest bardzo małe. Już dla N = 4 proces GC ma ponad 9000 stanów. Dla N = 5 sam proces Mem miałby równo 100 000 stanów, co wyklucza próby robienia czegokolwiek w CWB.
Szczególnie przykry jest drugi przykład w sekcji Inne modele. Okazuje się, że N = 4 jest zbyt małe, by własności w ogólności nieprawdziwe były w modelu niespełnione.