Kolokwium teoretyczne (2010) - rozwiązanie
Dla relacji R = ABCDE i zbioru zależności funkcyjnych AB -> C, C -> AE, D -> B, AD -> C, BCE -> A, BD -> E
- znajdź wszystkie klucze
- ustal w której jest postaci normalnej (i uzasadnij)
- (jeżeli już nie jest) sprowadź R do trzeciej postaci normalnej - jeżeli jest to możliwe bez utraty zależności funkcyjnych
Klucze: AD, CD (nie trzeba uzasadniać)
Relacja jest oczywiście w 1NF, nie jest natomiast w 2NF, bo istnieją zależności częściowe, które nie mają atrybutu głównego po prawej stronie, np. D->B (miło jest podać przykład zależności łamiącej 2NF)
Znajdujemy pokrycie minimalne. Łatwo wyeliminować zależności BCE->A (bo C->A) oraz AD->C (bo D->B i AB->C). Nie można natomiast zapomnieć jeszcze o uproszczeniu zależności BD->E do D->E (bo D->B). Pokrycie minimalne wygląda więc tak: AB->C, C->A, C->E, D->B, D->E.
Dla każdej zależności tworzymy tabelę, a że nigdzie nie ma klucza relacji, to dodajemy dodatkową tabelę z jednym z kluczy: ABC (C->A, AB->C), CE (C->E), BD (D->B), DE (D->E), AD (brak).
Dla relacji R = ABCDEFG i zbioru zależności funkcyjnych BD -> F, B -> A, CE -> DG, G -> E, C -> B, F -> A
- znajdź wszystkie klucze
- ustal w której jest postaci normalnej (i uzasadnij)
- (jeżeli już nie jest) sprowadź R do postaci normalnej Boyce'a-Codda - jeżeli jest to możliwe bez utraty zależności funkcyjnych
Klucze: CE, CG
Relacja jest oczywiście w 1NF, nie jest natomiast w 2NF, bo istnieją zależności częściowe, które nie mają atrybutu głównego po prawej stronie, np. C->B
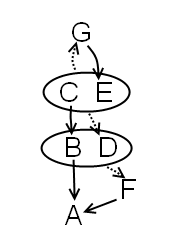
Które zależności łamią BCNF? Wszystkie poza CE->DG (możemy na nią oczywiście patrzeć jak na dwie zależności CE->D i CE->G). Uwaga, tylko ich możemy użyć do rozbicia relacji na mniejsze! Wolimy z naszej relacji wyrzucać atrybuty które nie mają strzałek wychodzących - wydzielenie atrybutu który występuje po lewej stronie zależności zazwyczaj powoduje ich utratę i mocno komplikuje rzutowanie zbioru zależności (jak nie ma strzałek wychodzących, to nie wygenerujemy za pomocą naszej zależności nic więcej - bo w żadnej innej zależności nie ma tego atrybutu po lewej stronie). W naszym przykładzie schemat postępowania wygląda tak:
- F->A (lub B->A) - tracimy zależność B->A; rzutowanie reszty jest trywialne
- BD->F - nic nie tracimy; rzutowanie jest trywialne
- C->B - nic nie tracimy; rzutowanie jest trywialnie
Warto zatrzymać się w tym miejscu i zastanowić nad zastaną sytuacją. Zostały nam atrybuty CDEG z zależnościami CE->D, CE->G i G->E. Tylko jedna z nich jest zła, bo częściowa, w kolejnym kroku musimy użyć zatem jej:
- G->E - tracimy zależność CE->G
i tu jest jedyny trudny fragment zadania - musimy zrzutować zbiór zależności na pozostające atrybuty (CDG). Jak to zrobić? Musimy domknąć zbiór naszych trzech zależności i zostawić tylko te z nich które nie używają E. Ale co tu możemy nowego stworzyć? Rozpatrując wszystkie pary po dwa razy (np. z CE->G i G->E mamy CE->E - nieciekawe, z G->E i CE->G mamy CG->G - nieciekawe) dostajemy tylko jedną dodatkową zależność: CG->D, która nie zawiera E i jest jedyną zależnością która zostaje nam w naszej tabeli CDG.
Finalnie mamy zatem tabele AF (F->A), BDF (BD->F), BC (C->B), EG (G->E) i CDG (CG->D).
Określenie które zależności straciliśmy w wyniku normalizacji nie jest takie proste. Formalnie powinniśmy tak naprawdę porównać dopełnienia zbiorów zależności początkowych i końcowych. Np. na koniec zastąpiliśmy zależność CE->D słabszą zależnością CG->D, więc faktycznie straciliśmy też zależność CE->D - nie wynika ona przecież z tych zależności jakie zostały. Nie wymagam jednak tego od Państwa, warto jednak wiedzieć kiedy w ogóle coś tracimy, a kiedy nie.
Zadania tego nie trzeba oczywiście opisywać tak szczegółowo jak ja to zrobiłem, ale ciąg kolejnych rozłożeń relacji powinien być widoczny i zbiór zależności po każdym rozłożeniu zaznaczony. Najlepiej użyć notacji drzewiastej jak robiliśmy na zajęciach.
Zaproponuj model związków encji dla bazy danych w której przechowywane będzie drzewo genealogiczne. Z każdą osobą musi być związane imię, nazwisko oraz data urodzenia. Ponadto baza danych musi pozwalać na:
- wypisanie wszystkich osób będacych w dowolnej relacji rodzinnej z daną osobą (np. wszystkie babcie, wszystkich wujków, najstarszego syna)
- wypisanie historii małżeństw danej osoby (data ślubu, nazwisko małżonki/małżonka)
- wypisanie dla danej osoby daty poznania się rodziców
Dodatkowo należy założyć, że związek małżeński łączy kobietę z mężczyzną.
Zaznacz na diagramie wszystkie związki między encjami, wskaż ich krotności oraz czy są wymagane. W każdej encji oznacz klucz główny (PK), klucze zewnętrzne (FK) oraz gwiazdką (*) atrybuty obowiązkowe.
Rozwiązanie było omówione na ćwiczeniach. Relacje jakie zaplanowaliśmy:
- Osoba (atrybuty: idosoby/pesel (PK), imię (*), nazwisko (*), data urodzenia (*))
- Mężczyzna, podklasa Osoba (brak atrybutów)
- Kobieta, podklasa Osoba (brak atrybutów)
- Poznanie (atrybuty: data poznania (*))
- Małżeństwo (atrybuty: data slubu (*), data rozwodu (o))
ze związkami:
- tata: Mężczyzna - Osoba (jeden do wielu)
- mama: Kobieta - Osoba (jeden do wielu)
- mąż: Mężczyzna - Małżeństwo (jeden do wielu identyfikujący)
- żona: Kobieta - Małżeństwo (jeden do wielu identyfikujący)
- poznajacy: Osoba - Poznanie (jeden do wielu identyfikujący)
- poznawany: Osoba - Poznanie (jeden do wielu identyfikujący)
UWAGA! TO NIE JEST ROZWIĄZANIE! Rozwiązanie powinno zawierać piękny diagram, taki jaki rysowaliśmy na zajęciach.