Zadania: cykle Eulera i Hamiltona

  1. Podać przykłady (możliwie prostych) grafów takich, że (a) istnieje cykl Eulera i Hamiltona, (b) nie istnieje ani cykl E. ani H. (c) istnieje cykl E., nie istnieje cykl H. (d) istnieje cykl H., nie istnieje cykl E.
  2. Dla jakich wartości n graf Kn (pełny graf n-wierzchołkowy) jest Eulerowski? a Hamiltonowski?
  3. Dla jakich wartości n,m graf Kn,m (pełny graf dwudzielny) jest Eulerowski? a Hamiltonowski?
  4. Ścieżka Eulera w danym grafie to ścieżka, która zawiera każdą krawędź grafu dokładnie raz. Graf jest półeulerowski, gdy zawiera ścieżkę Eulera. Jaki warunek powinny spełniać stopnie wierzchołków aby graf był półeulerowski? Sformułuj taki warunek, który jest wystarczający i konieczny, tzn. graf jest półeulerowski wtedy i tylko wtedy gdy spełnia Twój warunek. Wskazówka: skorzystaj z twierdzenia Eulera.
  5. Hiperkostka Qn to graf zdefiniowany rekurencyjnie: Q0=K1 czyli jest pojedynczym wierzcholkiem. Kostka Qn składa się z dwóch kopii kostki Qn-1 oraz dodatkowo łączymy krawędziami każdy wierzchołek z "pierwszej" kostki Qn-1 z jego kopią w "drugiej" kostce Qn-1, jak na rysunku:

    hiperkostka

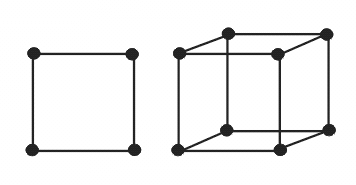
    Na przykład Q2 to kwadrat a Q3 możemy sobie wyobrazić jako sześcian: Q_2 i Q_3

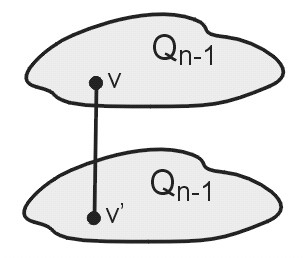
    (a) Udowodnij, że kostka Qn jest grafem dwudzielnym dla dowolnego n.
    (b) Udowodnij, że kostka Qn jest grafem hamiltonowskim dla dowolnego n>1.
    (c) Dla jakich wartości n kostka Qn jest grafem eulerowskim?.

.