Teoria liczb, semestr letni 2022/23
wykład: czwartek 14:15 — 15:45 (3150).
ćwiczenia: poniedziałek 12:15 — 13:45 (4050) oraz czwartek 16:15 — 17:45 (3150).
Usoswebowa strona
Podręczniki: Ireland, Rosen A Classical Introduction to Modern Number Theory, Białynicki-Birula, Skałba Lectures on number theory. Również warte przeczytania Steward, Tall Algebraic Number Theory and Fermat's Last Theorem.
Lista wykładów
- 2.03. Przegląd problemów otwartych: hipoteza Goldbacha, zera funkcji zeta Riemanna, bliźniacze liczby pierwsze, Wielkie Twierdzenie Fermata. Kongruencje: definicje, chińskie twierdzenie o resztach, grupy multiplikatywne Z_n^*, grupa Z_{p^e}^* jest cykliczna. (patrz np. [Rozdział 2, Białynicki-Birula, Skałba] lub [Rozdział 3-4, Ireland-Rosen])
- 9.03. Równość (x+y)^p = x^p + y^p i jej konsekwencje, twierdzenie Lucasa. Postulat Bertranda z dowodem (patrz np. Dowody z Księgi lub wikipedia)
- 16.03. Funkcja zeta Riemanna. Zbieżność dla rzeczywistego argumentu większego niż 1, granica (s-1)zeta(s) w s=1, funkcja zeta(s) przedłuża się do s > 0. Informacje o argumentach zespolonych i holomorficzności. Wzór produktowy. Gęstość Dirichleta, gęstość wszystkich liczb pierwszych to jeden. Sformułowanie twierdzenia Dirichleta. (źródło: Ireland-Rosen, podrozdział 16.1 i stwierdzenie 16.5.1)
- 23.03 Dowód Eisensteina prawa wzajemności reszt kwadratowych Gaussa. Symbol Jacobiego i symbol Hilberta (źródło: Białynicki-Birula, Skałba, rozdział 6 i ćwiczenia.).
- 30.03 Dowód twierdzenia Dirichleta, część pierwsza.
- 13.04 Dowód twierdzenia Dirichleta, dokończenie.
- 20.04 Teoria pierścieni liczbowych: pierścień O_K, ślad, istnienie bazy O_K, własności ideałów i ideałów pierwszych w O_K.
- 27.04 Wyróżnik pierścienia liczbowego. Rozkłady ideałów w pierścieniach liczbowych.
- 4.05 Równanie Pitagorasa, wielkie twierdzenie Fermata dla wykładnika n=4 oraz dla n=3 (początek).
- 11.05 Wielkie twierdzenie Fermata dla wykładnika n=3, dokończenie.
- 18.05 Krzywe eliptyczne: równania Weierstrassa oraz dodawanie punktów.
- 25.05 Krzywe eliptyczne: dowód łączności dodawania punktów.
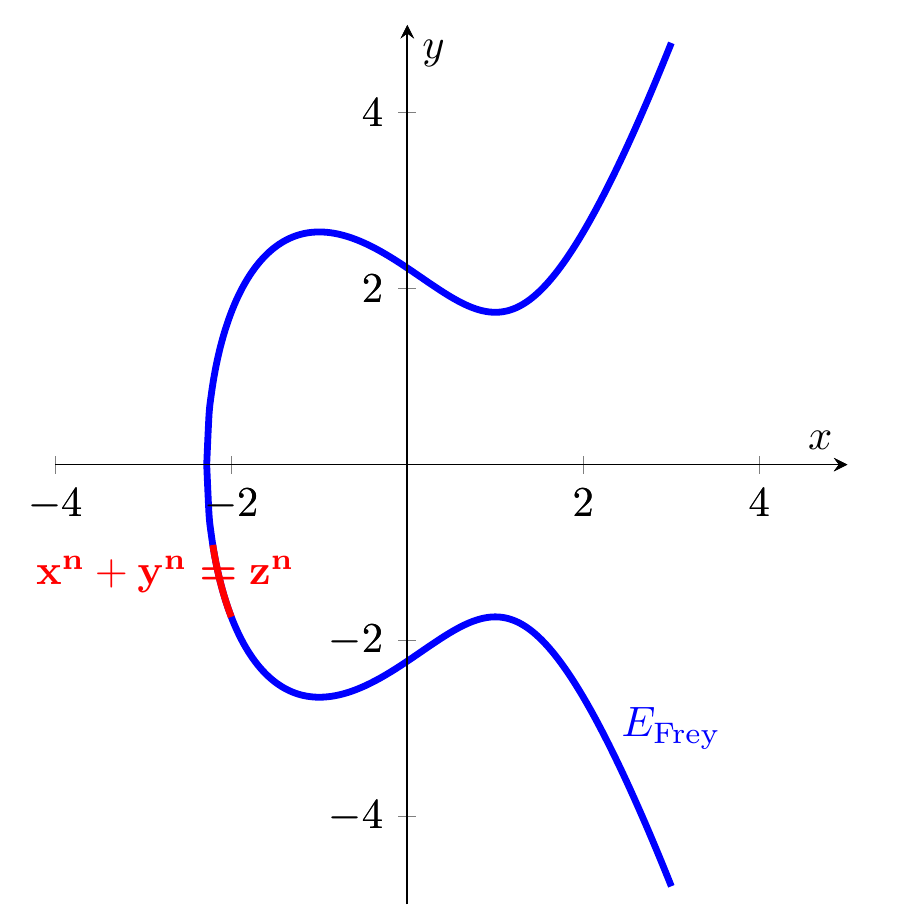
- 1.06 Modularność i nieco o dowodzie Wielkiego Twierdzenia Fermata. Skończoność grupy klas dla pierścieni liczbowych.
- 15.06 Oszacowanie Minkowskiego, twierdzenie Minkowskiego z dowodem. Przykładowe obliczenia grup klas.
Zadania i rozwiązania
Zadania domowe
Ogólne zasady egzaminu
Termin: 19 czerwca, początek o 14, sala 3320.
Domyślnie, do egzaminu dopuszczone są wszystkie osoby, które mają co najmniej 3 punkty za zadania domowe (wliczając zadanie numer 5). Osoby mające mniej punktów, a zainteresowane zaliczeniem, proszę o szybki kontakt mailowy.
Zadania na egzaminie pisemnym będą dwóch rodzajów:
- "wykładowe", typu "Sformułuj twierdzenie .... Co z niego wynika na
przykładzie ..." albo "Zdefiniuj pojęcie .... Czy jest zawsze prawdą, że .... spełnia ..."
Będę pytać o główne twierdzenia, nie jakieś lematy do lematu. Lista
wykładów na stronie przedmiotu daje dobre przybliżenie, czego się można
spodziewać.
- "ćwiczeniowe", typu "Rozwiąż równanie ...", "Pokaż zbieżność ...", "Oblicz
grupę punktów krzywej eliptycznej ..."
Tu zadania będą bardzo podobne do tych z serii zadań domowych.
Wyniki ukazały się w USOSweb 21.06 postaci punktów oraz ocen (w zakładce sprawdziany). Osoby zainteresowane podwyższeniem oceny mogą umawiać się na egzamin ustny, pisząc do mnie do 12:00 w dniu 24.06 maila z proponowanymi terminami w tygodniu 26.06 -- 1.07. Egzamin ustny polega na około godzinnej rozmowie na temat zagadnień z wykładu i koncentruje się na sprawdzeniu Państwa zrozumienia (nie zapamiętania) materiału; oczywiście jest dostosowany do oceny: na niższą pytam o mniej rzeczy. Z egzaminu nie można dostać niższej oceny niż z pisemnego.
Ogólne zasady oceniania
Na zaliczenie ćwiczeń: zadania domowe pisemne, 5 serii po jednym zadaniu.
Zadania będą ogłaszane tydzień wcześniej, pierwsza seria około trzeciego
tygodnia zajęć.
Ocena końcowa na podstawie egzaminu.