The goal of this page is to prove the following theorem.

Theorem. Let  and let be an mso formula over the vocabulary of graphs, i.e. using a binary relation .  There is a linear time algorithm which inputs a tree decomposition of width and decides if the underlying graph satisfies .

Recall sourced graphs, the algebraic definition of tree decompositions that was described here. Define to be the following ranked alphabet. For every sourced graph with at most vertices and at most sources contained in we have a rank zero letter. For every set of size at most we have a rank two letter . A tree over this alphabet can be viewed as a term in the algebra of sourced graphs, which generates some sourced graph. The following

Lemma 1. For every tree decomposition of width at most one can compute in linear time a tree over alphabet which generates the same graph (a graph is interpreted as a sourced graph with no sources).

Proof. A simple bottom-up pass through the tree decomposition, the same as is used in the theorem here. The only additional observation is that, by reusing source names, we can be sure that source names are enough.

Recall that for a given tree automaton, checking if an input tree is accepted can be done in linear time. Therefore, the theorem from the beginning of this page follows from Lemma 1 and Lemma 2 below.

Lemma 2. Let and let be an mso formula over the vocabulary of graphs, i.e. using a binary relation . There is a tree automaton such that for every tree over the ranked alphabet the following conditions are equivalent:

1. the tree 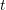is accepted by ;
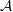2. the graph generated by 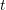satisfies .

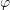Proof. Recall that over trees, mso and tree automata have the same expressive power. Therefore it suffices to find a formula of mso over trees such that is true in a tree if and only if the graph generated by the tree satisfies .

We assume that for every rank zero letter there is an enumeration of the at most vertices that appear in the sourced graph which uses numbers . Consider a is a tree over . For a leaf of the tree and , define to be the vertex in the graph generated by which corresponds to the -th vertex in the label of . The vertex might be undefined if is not part of the enumeration in the label of . Furthermore it might be the case that for some , this is because of the fuse operations. This definition is illustrated below (the green numbers are the enumerations of the vertices in the leaves).

Furthermore, the equality can be tested in mso on the tree in the following sense.

Claim. For every there is an mso formula which selects a pair of nodes in the tree if and only if

Proof of the claim. The formula says that there is some source name and a node such that:

• is an ancestor of both and
• on the path from to , the vertex corresponding to 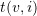is present all the time as an source with name ;
• on the path from to , the vertex corresponding to 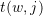is present all the time as an source with name .

This completes the proof of the claim.

In a similar way, we can write an mso formula which selects a pair of nodes in the tree if and only if the underlying graph has an edge from to . Once we have these formulas, we can simulate mso on the graph generated by using mso on the tree itself. The idea is that instead of quantifying over a set of vertices in the generated graph, we can quantify over sets  of nodes in , with

   

Using the formulas from the claim and analogue for edges, we can interpret the tuple as a set of vertices in the graph, and test the edge relationship between these vertices.