8. Automata with infinite alphabets
Define a data word to be a word over an alphabet of the form ![]() , where
, where ![]() is a finite set, and
is a finite set, and ![]() is an infinite set. The first coordinate is called the label and the second coordinate is called the data value. The idea is we will be able to test labels explicitly by asking questions like “does the second letter have
is an infinite set. The first coordinate is called the label and the second coordinate is called the data value. The idea is we will be able to test labels explicitly by asking questions like “does the second letter have ![]() as its label?” but we will only be allowed to test the data value for equality e.g. ask “do the third and fifth letters have the same data value?”
as its label?” but we will only be allowed to test the data value for equality e.g. ask “do the third and fifth letters have the same data value?”
By abuse of notation, we assume that a word over the alphabet ![]() is also a data word, here there are no labels. Here are some examples of languages of data words, in all of these examples we use no labels:
is also a data word, here there are no labels. Here are some examples of languages of data words, in all of these examples we use no labels:
- the first data value is the same as the last data value
- some data value appears twice
- no data value appears twice
- the first data value appears again
- consecutive data values are different
In this lecture, we introduce automata models for data words that capture the properties above. We begin with a nondeterministic register automaton.
Definition. A nondeterministic register automaton consists of:
• a finite alphabet ![]() for the labels;
for the labels;
• a finite set ![]() control states;
control states;
• a finite set ![]() of register names;
of register names;
• an initial state ![]() and a set of accepting states
and a set of accepting states ![]() ;
;
• a transition relation
![]()
subject to the equivariance condition described below.
The automaton is used to accept or reject data words where the alphabet is ![]() . After processing part of the input, the automaton keeps track of a configuration, which consists of a control state and a register valuation (i.e. a partial function from register names to atoms). Initially, the configuration consists of the initial state and a completely undefined register valuation. The configuration is then updated according to the transition relation
. After processing part of the input, the automaton keeps track of a configuration, which consists of a control state and a register valuation (i.e. a partial function from register names to atoms). Initially, the configuration consists of the initial state and a completely undefined register valuation. The configuration is then updated according to the transition relation ![]() , and the automaton accepts if at the end of the word the control state belongs to the accepting set.
, and the automaton accepts if at the end of the word the control state belongs to the accepting set.
The only issue is how to describe the transition relation. Since the space of configurations is infinite, the transition relation cannot be any relation. We choose the following restriction, called equivariance: the transition relation can only compare data values with respect to equality. Equivariance can be formalized in two different ways below:
- Semantic equivariance. Suppose that
 is a bijection on the data values
is a bijection on the data values 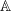 . We can apply
. We can apply  to configurations in the natural way, and therefore also to triples in the transition relation
to configurations in the natural way, and therefore also to triples in the transition relation 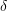 . We say that
. We say that 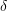 is semantically equivariant if
is semantically equivariant if 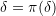 holds for every bijection
holds for every bijection  of the atoms.
of the atoms. - Syntactic equivariance. We say that
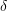 is syntactically equivariant if it can be defined by a finite Boolean combination of statements of the following types:
is syntactically equivariant if it can be defined by a finite Boolean combination of statements of the following types:
• the control state in the source (respectively, target) configuration is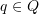 ;
;
• the label in the input letter is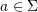 ;
;
• the data value is undefined in register of the source configuration (respectively, target configuration);
of the source configuration (respectively, target configuration);
• the data value in the input letter equals the contents of register in the source configuration (respectively, target configuration);
in the source configuration (respectively, target configuration);
• the data value in register of the source configuration (respectively, target configuration) equals the data value in register
of the source configuration (respectively, target configuration) equals the data value in register  of the source configuration (respectively, target configuration).
of the source configuration (respectively, target configuration).
The advantage of semantic equivariance is that the definition is short. The advantage of syntactic equivariance is that it shows how the transition relation can be represented. The following straightforward lemma is given without proof.
Lemma. Semantics and syntactic equivariance are the same.
This completes the definition of nondeterministic register automata: the transition relation is required to be equivariant in either of the two equivalent senses defined above. The transition relation is called deterministic if the source configuration and the input letter determine uniquely the target configuration.
Recall the five example languages. Deterministic register automata can 1,4,5. Nondeterministic register automata can do 1,2,4,5. In particular, deterministic register automata are strictly weaker than nondeterministic ones, and nondeterministic ones are not closed under complement.
Theorem. Emptiness is decidable for nondeterministic register automata, but universality is not.
Proof. When talking about decidability, we assume that the transition function is represented according to the syntactic equivariance condition.
Let us begin with the decidability argument. Define the equality type of a configuration to be the following information: the control state, which registers are defined, and which registers store the same data value. It is not difficult to see that if a configuration of some equality type is reachable in the automaton, then all configurations of this equality type are also reachable. The algorithm for nonemptiness computes the equality types of reachable configurations. Intitially, we have the equality type of the unique initial configuration, which can be easily computed. If we have the equality type of some configuration, we can easily compute the equality types of all configurations reachable from it in one step; thus finishing the description of the algorithm.
Let us do the undecidability. We reduce from the halting problem. Suppose that we have a Turing machine which is an instance of the halting problem. We encode a run of a Turing machine as a data word according to the following following picture:
Each letter encodes a single cell in a single configuration. The word represents a sequence of configurations, padded with blanks so that they all have the same length, and separated by a letter #. The labels are used to store the contents of the cell (light blue), plus the control state (dark blue) of the head if the head happens to be over that cell. Finally, each cell gets a unique identifier, a data value (red). We claim that there is a nondeterministic register automaton which accepts a data word if and only if it is not an encoding of an accepting run of the Turing machine, and therefore solving universality for this automaton also solves the halting problem. To prove the claim, we list the mistakes that can happen in a word that does not encode an accepting run of a Turing machine:
1. The data values identifying the cells are chosen wrong. This means that either:
• the separator # is used with more than one data value; or
• some data value ![]() appears in two different places, with successor positions having data values
appears in two different places, with successor positions having data values ![]() .
.
The first condition can be tested using one register, the second condition using two registers.
2. There is a mistake between two consecutive configurations. Assuming the identifiers are chosen correctly, this can be tested using only one register, to tell which cells correspond to which ones in the following configuration.
3. The first configuration is not initial, or the last configuration is not accepting. For this, no registers are needed.
![]()
Leave a Reply